Собственно-случайная выборка для определения средней

Пусть из генеральной совокупности распределения признака, в которой характеризуется как варианты и частоты

Таблица 1

xi	Ni	Pi
x1 x2 ….. xn	N1 N2 ….. Nm	, ,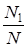

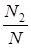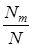
Для оценки неизвестной генеральной средней образуется повторная выборка объема N. Обозначим через x₁,x₂,…,x_n случайные величины, выражающие значения интересующего нас признака при отборе 1-го, 2-го, n-го членов выборки. Каждый раз после возврата отобранного члена восстанавливается первоначальный состав генеральной совокупности, поэтому случайные величины x₁,x₂,…,x_n одинаково распределены и независимы.

Выборочная средняя повторной выборки, образованной для оценки неизвестной генеральной средней -это среднее арифметическое случайных величин x₁,x₂,…,x_n.

.

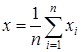Таким образом, она является суммой - независимых одинаково распределенных случайных величин, имеющих абсолютные центральные моменты 3 порядка поскольку каждая из случайных величин принимает лишь конечное значение и эти значения ограничены, поэтому согласно следствия из теоремы Ляпунова, выборочная средняя повторной выборки достаточно большого объема распределена по нормальному закону. Нужно найти параметры этого распределения. Для этого вычислим математическое ожидание и дисперсию.

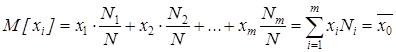(1)

Также найдем дисперсию

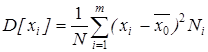(2)

Обозначим это значение как 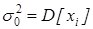. Таким образом, математическое ожидание и дисперсия одинаковы и равны генеральной средней 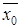и генеральной дисперсии 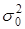. Математическое ожидание выборочной средней равно генеральной средней, а дисперсия выборочной средней будет равна ;

;

.

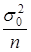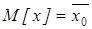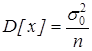Для оценки генеральной средней образовывают из этой же генеральной совокупности бесповторную выборку объема N случайной величины y₁,y₂,…,y_n, выражающие значения, интересующего нас признака при отборе 1-го, 2-го, n-го члена выборки одинаково распределены и их закон распределения задается той же таблицей №1. Т.е. случайные величины x₁ и y₁ имеют один и тот же закон распределения.

.

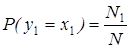Т.е. доказано, что случайные величины y₁,y₂ распределены одинаково. Также доказано, что такой же закон имеют и оставшиеся величины, закон распределения их распределения характеризуется таблицей №1, т.к. величины y₁,y₂,…,y_n одинаково распределенные величины, то их математические ожидания также равны генеральной средней, а дисперсия равна генеральной дисперсии. В отличие от повторной выборки y₁,y₂,…,y_n, зависимые случайные величины. Выборочная средняя у бесповторной выборки является средней арифметической случайных величин y₁,y₂,…,y_n.

.

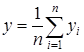Выборочная средняя бесповторной выборки достаточно большого объема N распределена по нормальному закону, хотя и случайные величины y_i зависимые.

1-й параметр случайной величины y равен генеральной средней .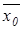

.

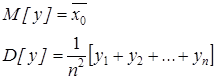
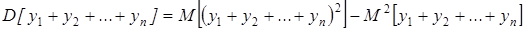
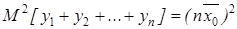
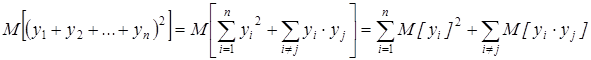Случайные величины y_i² также распределены одинаково и поэтому имеют одинаковые математические ожидания, поэтому

;

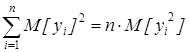Математическое ожидание y_i можно записать как

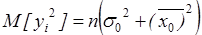(3)

Рассмотрим произведение y₁y₂, значение этой случайной величины является произведение всевозможных комбинаций значений случайных величин y₁,y₂. Вероятности значений случайной величины находятся по теореме умножения вероятностей для зависимых событий, учитывая при этом число членов генеральной совокупности с соответствующим значением признака.

Представим это в таблице №2

y1	y2	y1y2
x1 x1 …………………. x1	x1 x2 ……………………….. xm	x12 x1x2 ………………………….. x1xm	…………………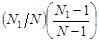
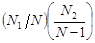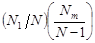
x2 x2 …………………. x2	x1 x2 …………………. xm	x1x2   x22 …………………. x2xm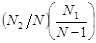
………………….	……………………..	……………………….	………………
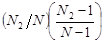
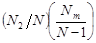
………………… xm xm … xm	…………………….. x1 x2 ……………………….. xm	………………………. xmx1 xmx2 ………………………….. xm2	………………

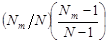
В соответствии с определением находим математическое ожидание. Перемножаем значения 3-го и4-го столбца и складываем, вынося общий множитель за скобки, находим, что

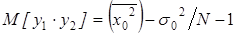
При любых i и j случайные величины y_i×y_j имеют такие же математические ожидания, поэтому сумма M[y_i×y_j] будет равна

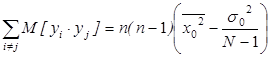
Соединяем полученные результаты

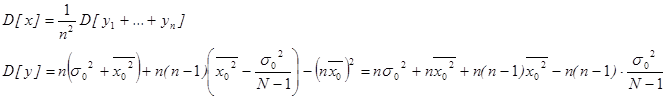
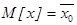
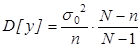(5)

Выборочная средняя бесповторной выборки является случайной величиной распределения по нормальному закону с параметрами.

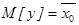, а дисперсия определяется по формуле (5).

В формуле (5) заменим N-1 на N, т.е.

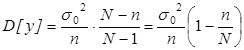(6)

При повторном и бесповторном отборе членов выборочная средняя является несмещенной и состоятельной оценкой генеральной средней.