Решение

1) Для генеральной средней

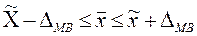
D_мв= tm_мв

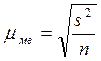n = 10

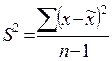
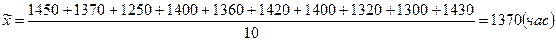
S² = ((1450-1370)² + (1370-1370)² + (1250-1370)² + … + (1430-1370)²): (10-1) = 3620

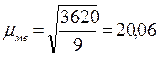
Для определения t исчислим S_t

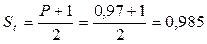
K = n-1 = 10-1 = 9

По таблице распределения Стьюдента при S_t = 0,985 и К = 9 коэффициент доверия t = 2,6

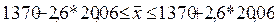
1317,8£ 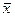£1422,2 (час.)

Следовательно, с вероятностью 0,97 можно утверждать, что генеральная средняя колеблется в пределах от 1317,8 до 1422,2 часа.

2. Для определения вероятности того, что отклонение генеральной средней от выборочной средней не превышает 48 часов, имеем следующие данные: D_мв = 48 час m_мв = 20,06 (см. п.1).

Отсюда t фактическое =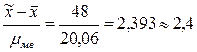

Пользуясь таблицей распределения Стьюдента, определяется значение функции S_t при t = 2,4 и К = 9.

S_t = 0,98

Вероятность того, что отклонение генеральной средней от выборочной средней не превзойдет 48 час.

P = 2 S_t – 1 = 2*0,98 – 1 = 0,96

Вероятность того, что ошибка будет превышать 48 час.

P = 1-0,96 = 0,04

Таким образом, вероятность того, что средней срок службы ламп для всей партии отличается от полученного по выборке не более чем на 48 часов, равна 0,96 или 96%, а вероятность того, что средний срок службы будет отличаться от выборочного более, чем на 48 часов, равна 0,04 или 4%.