Алгоритм расчётов по проведению однофакторного дисперсионного анализа вручную

1. Показать возможность применения к экспериментальным данным дисперсионного анализа при уровне значимости 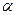, применив критерий Бартлетта. 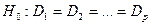; 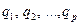– количество наблюдений на уровнях 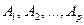соответственно; 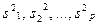– исправленные дисперсии на уровнях 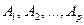соответственно.

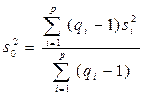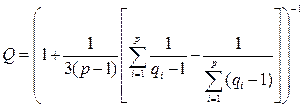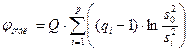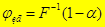, где F (x) – функция распределения Хи-квадрат (Пирсона) с (p –1) степенями свободы.

При одинаковом числе наблюдений на всех уровнях применить критерий Кочрена.

2. Найти средние для каждого уровня фактора 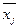и общее среднее .

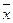3. Составить расчётную таблицу, обозначив 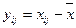отклонения наблюдений 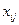от общего среднего 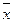. 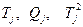- суммы отклонений и квадратов отклонений по столбцам расчётной таблицы.

Пусть уровней фактора 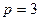, число наблюдений на каждом уровне одинаковое .

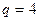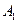
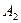
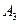
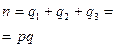
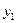
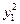
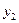
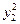
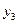
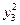
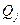
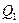
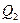
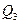
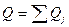
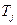
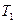
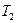
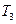
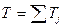
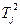
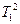
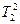
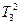
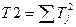
1. Найти суммы факторную, общую, остаточную:

; ; .

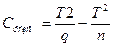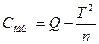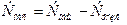1. Найти дисперсии факторную и остаточную: ; .
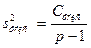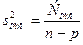2. Вычислить наблюдаемое значение статистики критерия Фишера .
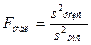3. Найти критическую точку по таблице критических точек распределения Фишера – Снедекора 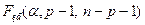или функцией 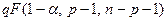в системе Маткад.
4. Принять или отклонить нулевую гипотезу о незначимом отличии факторной и остаточной дисперсий, т.е. о незначимом влиянии фактора.

Замечание. При разном количестве наблюдений на разных уровнях фактора по-другому вычисляется только факторная сумма

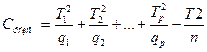. Все остальные вычисления проводятся так же, как и при одинаковом количестве наблюдений на всех уровнях фактора.