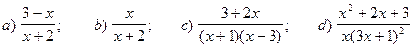 ;
;
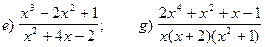 .
.
Решение примера 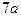 : Поскольку дробно-рациональная функция представляет собой неправильную дробь (степень многочлена числителя не меньше степени многочлена знаменателя), выделим из дроби целую часть и правильную дробь, у которой степень многочлена числителя меньше степени многочлена знаменателя. Процесс выделения проыведем с помощью деления в столбик:
: Поскольку дробно-рациональная функция представляет собой неправильную дробь (степень многочлена числителя не меньше степени многочлена знаменателя), выделим из дроби целую часть и правильную дробь, у которой степень многочлена числителя меньше степени многочлена знаменателя. Процесс выделения проыведем с помощью деления в столбик:
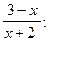
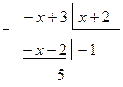
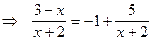 .
.
Таким образом, имеем:
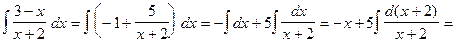
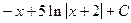 .
.
При вычислении был использован табличный интеграл
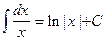 .
.
Решение примера  :
:
Как и в примере  , неправильную дробь с помощью деления в столбик можно представить, как сумму целой части и правильной дроби. Однако вместо деления в столбик мы воспользуемся почленным делением дроби:
, неправильную дробь с помощью деления в столбик можно представить, как сумму целой части и правильной дроби. Однако вместо деления в столбик мы воспользуемся почленным делением дроби:
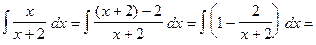
 .
.
Здесь был использован табличный интеграл 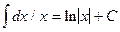 .
.
Решение примера  :
:
Рассматриваемая дробь является правильной дробью, однако ввиду того, что знаменатель разлагается на простые множители, удобно саму дробь разложить на простые дроби. Воспользуемся для этого методом неопределенных коэффициентов:
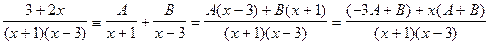 .
.
В силу тождественного равенства левой и правой дроби, соответствующие коэффициенты числителей (левой и правой дроби) должны совпадать. Откуда имеем:
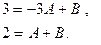
Решаем полученную систему двух уравнений и находим неизвестные коэффициенты.
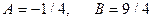
Таким образом, заданная правильная дробь представляется суммой простых дробей:
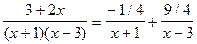 ,
,
откуда 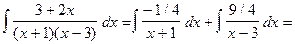
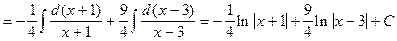 .
.
Здесь опять был использован табличный интеграл 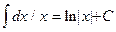 .
.
Решение примера  :
:
Заданная дробно-рациональная функция 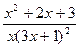 является правильной дробью. Методом неопределенных коэффициентов разложим ее на сумму простых дробей:
является правильной дробью. Методом неопределенных коэффициентов разложим ее на сумму простых дробей:
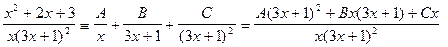 .
.
Приравнивая коэффициенты перед одинаковыми степенями 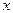 числителей левой и правой дроби, получаем систему уравнений для коэффициентов
числителей левой и правой дроби, получаем систему уравнений для коэффициентов 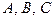 :
:
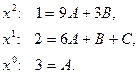
Решая систему, находим коэффициенты:
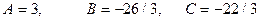 . Таким образом, имеем разложение:
. Таким образом, имеем разложение:
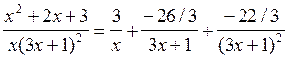 ,
,
откуда
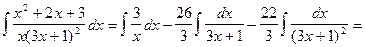
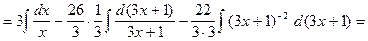
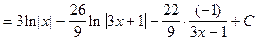 .
.
Здесь опять использовался табличный интеграл 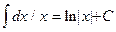 .
.
Решение примера  :
:
Дробно-рациональная функция является неправильной дробью. Делением в столбик, выделяем из нее целую часть и правильную дробь:
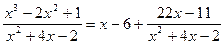 .
.
При этом искомый интегра равен:
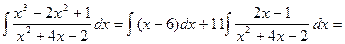
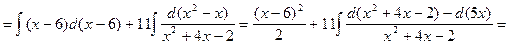
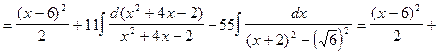
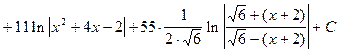 .
.
Здесь был использован метод интегрирования квадратного трехчлена, который применялся при решении примера 6. Из табличных интегралов использовались:
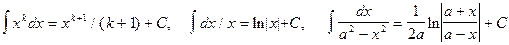 .
.
Покажем, также как производилось деление в столбик:
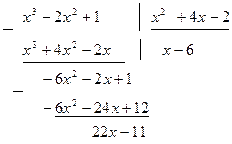 .
.
Решение примера 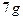 :
:
Заданная дробно-рациональная функция  представляет собой неправильную дробь. Делением в столбик выделяем из нее целую часть и правильную дробь:
представляет собой неправильную дробь. Делением в столбик выделяем из нее целую часть и правильную дробь:
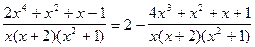 .
.
Методом неопределенных коэффициентов правильную дробь разлагаем на простые дроби:
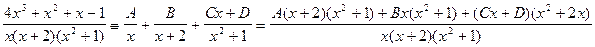 Приравнивая коэффициенты числителей при одинаковых степенях
Приравнивая коэффициенты числителей при одинаковых степенях 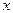 левой и правой дроби, получим систему уравнений для нахождения коэффициентов:
левой и правой дроби, получим систему уравнений для нахождения коэффициентов:
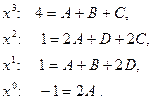
Решая систему, находим коэффициенты:
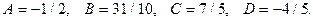
Искомый интеграл представляется в виде:
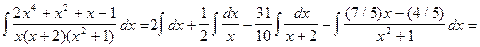
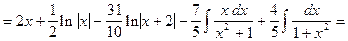
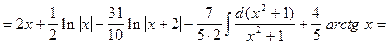
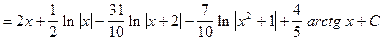 .
.
Из табличных были использованы интегралы:
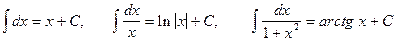 .
.
Покажем еще, как производилось деление в столбик:
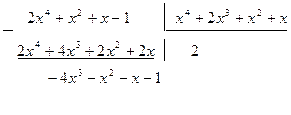 .
.
 2015-10-16
2015-10-16 586
586








