4.1 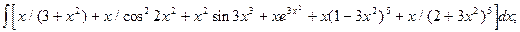
4.2 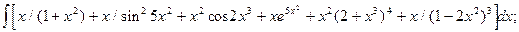
4.3 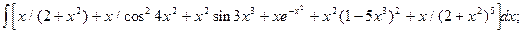
4.5 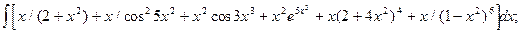
4.6 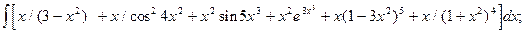
4.7 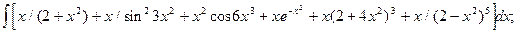
4.8 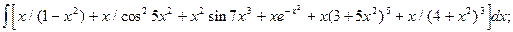
4.9 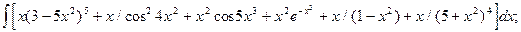
4.10 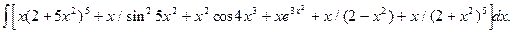
Пример 4. Вычислить неопределенный интеграл
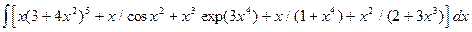 .
.
Искомый интеграл равен сумме следующих интегралов:
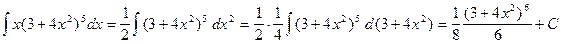 ,
,
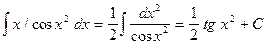 ,
,
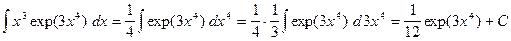 ,
,
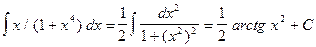 ,
,
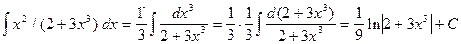 .
.
Здесь переменная 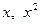 или
или 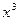 вносились под знак дифференциала с учетолм свойства дифференциала
вносились под знак дифференциала с учетолм свойства дифференциала 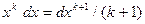 . При вычислении интегралов были использованы следующие табличные интегралы:
. При вычислении интегралов были использованы следующие табличные интегралы:
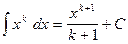 ,
, 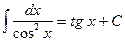 ,
, 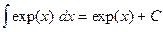 ,
,
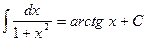 ,
, 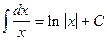 ,
,
а также свойство интеграла
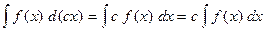 , где
, где 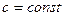 .
.
Задача 5. Вычислить неопределенный интеграл
5.1 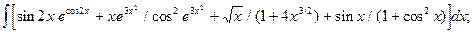
5.2 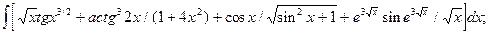
5.3 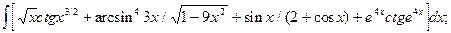
5.4 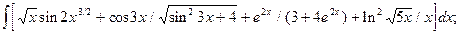
5.5 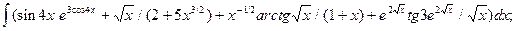
5.6 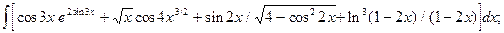
5.7 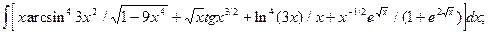
5.8 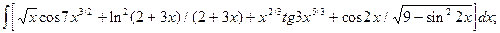
5.9 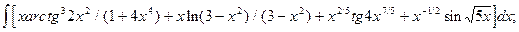
5.10 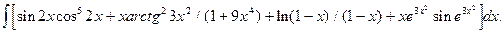
Пример 5. Вычислить неопределенный интеграл
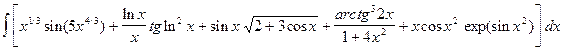 Искомый интеграл равен сумме следующих интегралов:
Искомый интеграл равен сумме следующих интегралов:
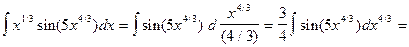
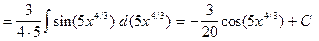 ,
,
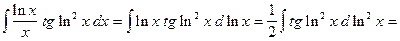
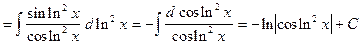 ,
,
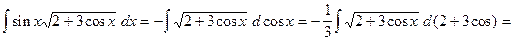
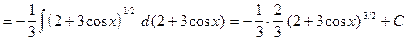 ,
,
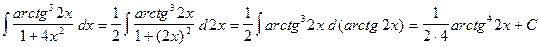 ,
,
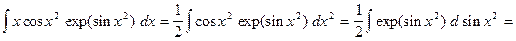
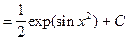 .
.
 Здесь для вычисления интегралов были использованы свойства дифференциала:
Здесь для вычисления интегралов были использованы свойства дифференциала:
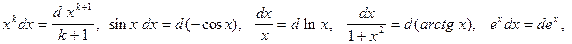 свойство интеграла:
свойство интеграла:
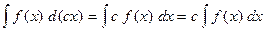 , где
, где 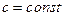 ,
,
а также табличные интегралы:
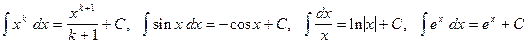 .
.
Задача 6. Проинтегрировать квадратный трехчлен
6.1 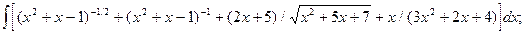
6.2 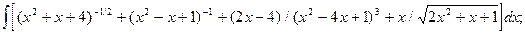
6.3 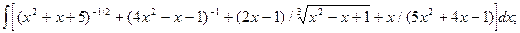
6.4 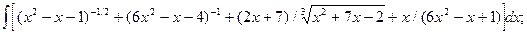
6.5 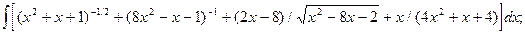
6.6 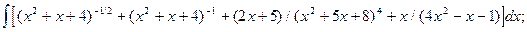
6.7 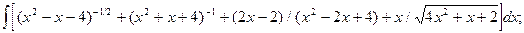
6.8 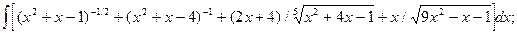
6.9 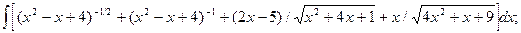
6.10 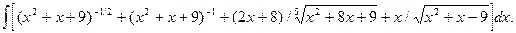
 2015-10-16
2015-10-16 367
367








