Свойство 1
Если ряды 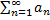 (1) и
(1) и 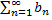 (2) сходятся, то и их суммы равны соответственно S и σ, то ряд
(2) сходятся, то и их суммы равны соответственно S и σ, то ряд 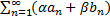 (3) сходится, при этом его сумма равна
(3) сходится, при этом его сумма равна 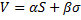 .
.
Доказательство.
Пусть 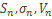 n-е частичные суммы соответственно рядов (1),(2),(3). Тогда
n-е частичные суммы соответственно рядов (1),(2),(3). Тогда 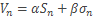 . Поскольку
. Поскольку 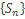 и
и 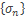 сходятся, то последовательность
сходятся, то последовательность 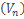 имеет конечный предел по свойству сходящихся последовательностей, то есть ряд (3) сходится и справедливо
имеет конечный предел по свойству сходящихся последовательностей, то есть ряд (3) сходится и справедливо 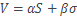 .
.
Свойство 2
Если сходится ряд 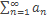 (1), то сходится ряд
(1), то сходится ряд 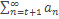 . (2)
. (2)
Данный ряд называют t -м остатком ряда (1). Верно и обратное: если при фиксированном t ряд (2) сходится, тогда и ряд (1)сходится.
Доказательство.
Пусть 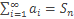 n -я частичная сумма ряда (1) и
n -я частичная сумма ряда (1) и 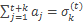 k -я частичная сумма ряда (2). Тогда
k -я частичная сумма ряда (2). Тогда 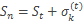 , где
, где 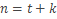 . (*).
. (*).
Если ряд (1) сходится, то 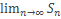 , причем конечный, таким образом из равенства (*) следует, что при фиксированном t, существует конечный предел последовательности
, причем конечный, таким образом из равенства (*) следует, что при фиксированном t, существует конечный предел последовательности 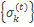 , при
, при 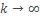 , то есть ряд (2) сходится.
, то есть ряд (2) сходится.
Обратное утверждение: если 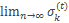 и он конечен, при фиксированном t, то существует конечный
и он конечен, при фиксированном t, то существует конечный 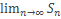 .
.
 2015-10-16
2015-10-16 2023
2023








