Свойство 3

Если ряд 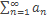(1) сходится, то ряд 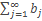(2), полученный путем группировки членов ряда (1) без изменения порядка их расположения, также сходится и его сумма равна сумме ряда (1).

Доказательство.

Пусть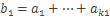

,

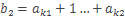где 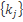– строго возрастающая последовательность натуральных чисел.

Пусть 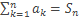, , 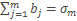тогда 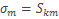. Так как 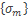–подпоследовательность сходящейся последовательности 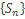, то 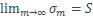, где S-сумма ряда (1).