I. Метод обратной матрицы

В матричной форме система уравнений (4) имеет вид (3). Пусть матрица системы А (5) является невырожденной, т.е. существует обратная матрица А^-1 (1). Умножив обе части этого уравнения слева на А^-1, получаем решение системы (4) в матричной форме: Х= А^-1В (6).

Пример: Решить методом обратной матрицы систему уравнений:

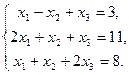
Решение: 1)Обозначим

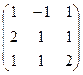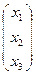А= ; Х= ; В= .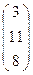

2) В матричной форме данная система имеет вид: АХ=В. Найдем определитель :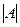

= = = = =

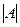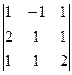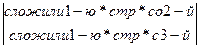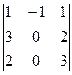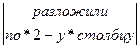= (-1)·(-1)^{1+2 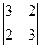=}9-4=5 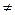0.

Матрица не вырожденная и существует обратная матрица А^-1.

3) Матрицу А^-1 находим по формуле (1). Получим:

А^-1= .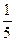

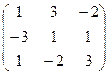4) По формуле (6):

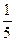
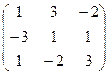
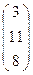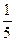
Х= А^-1В= = = 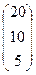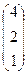, т.е. решение системы (4;2;1)

5) При подстановке полученных значений, получено верное тождество.

Часть