II. Метод Крамера

Теорема (правило Крамера). Пусть Δ — определитель матрицы — определитель матрицы системы А, а Δ _j — определитель, полученный из определителя Δ заменой j-го столбца столбцом свободных членов В. Тогда, если Δ 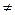0, тосистема линейных уравнений (4) имеет единственное решение, определяемое по формулам

x_i = Δ_j/ Δ, j= 1,2,…,n. (7)

Формулы вычисления неизвестных (7) носят название формул Крамера.

Правило Крамера можно использовать, только когда определитель системы Δ не равен нулю.

Пример: Решить, используя правило Крамера, систему уравнений:

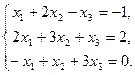
Решение:

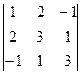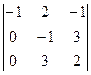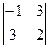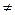Δ= = = =-11 0

Вычислим дополнительные определители и значения неизвестных:

Δ₁= 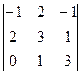= = 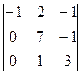- =-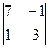22; x ₁ = Δ ₁ / Δ = (-22)/(-11)= 2.

Δ₂= 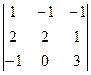= = 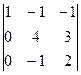=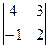11; x₂ = Δ₂ / Δ = 11/(-11)=-1.

Δ₃= 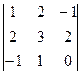= = 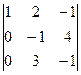=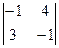-11; x ₃ = Δ ₃ / Δ = (-11)/(-11)=1.

Путем подстановки можно проверить, что полученное решение Х=(2,-1,1) является верным.