Случайные величины
Величину называют случайной, если в результате испытания она примет лишь одно возможное значение, заранее не известное и зависящее от случайных причин.
Случайная величина, принимающая отдельные возможные значения с определенными вероятностями, называется дискретной случайной величиной.
Непрерывной, называется случайная величина, которая может принимать все значения из некоторого промежутка.
Дискретные случайные величины
Табличный закон распределения
Соответствие между отдельными возможными значениями и их вероятностями называется законом распределения дискретной случайной величины.
Задается закон распределения дискретной случайной величины в виде соответствующей таблицы, состоящей из двух строк; первое указывает возможные значения, а вторая – их вероятности:
| Х | х1 | х2 | ….. | хn |
| Р | p1 | p2 | ….. | p pn |
(1)
В одном испытании случайная величина принимает только одно возможное значение, то события X=x1, X=x2, …, X=xn образуют полную группу, т.е. сумма их вероятностей равна единице:
p1 + p2 +…+ pn =1. (2)
Биномиальное распределение
Пусть производится n независимых испытаний, и в каждом из них событие А может либо появиться, либо не появится. Пусть также вероятность р появления события А в каждом испытании постоянна. В качестве дискретной случайной величины Х рассмотрим число появления события А в этих n испытаниях. Очевидно, что х1=0, х2=1, х3=2, …, хn+1=n. Вероятности этих возможных значений k даются формулой Бернулли:
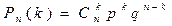 . (3)
. (3)
где 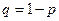 - вероятность противоположного события (непоявления события А в одном испытании). Формула (3) представляет собой аналитическую форму закона распределения случайной величины (числа появления события А в n независимых испытаниях), которое называется биномиальным; правая часть в (3) представляет собой общий член разложения бинома Ньютона. Используя формулу (3) можно составить таблицу биномиального распределения.
- вероятность противоположного события (непоявления события А в одном испытании). Формула (3) представляет собой аналитическую форму закона распределения случайной величины (числа появления события А в n независимых испытаниях), которое называется биномиальным; правая часть в (3) представляет собой общий член разложения бинома Ньютона. Используя формулу (3) можно составить таблицу биномиального распределения.
Сумма всех вероятностей биномиального распределения равна единице, т.е.
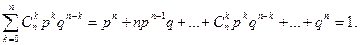 (4)
(4)
Пример: Банк выдает 5 кредитов. Вероятность невозврата кредита равна 0,2 для каждого из заемщиков. Составить таблицу закона распределения количества заемщиков, не вернувших кредит по окончании срока кредитования.
Решение. Примем за А событие невозврата кредита. Так как заемщики действуют независимо, то выдачу кредитов можно считать за n=5 независимых событий. Вероятность невозврата k кредитов из 5 описывается биномиальным распределением (3), где р=0,2, q=0,8, k принимает значения от нуля до 5. Придавая последовательно в формуле (3) k значения от нуля до 5 и используя формулы для расчета 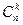 , получаем:
, получаем:
X 5 4 3 2 1 0
P 0,00032 0,0064 0,0512 0,2048 0,4096 0,32768
Распределение Пуассона
Пусть в каждом из n производимых испытаний вероятность появления события А равна р. Для случая малых значений р и больших значений n используется асимптотическая формула Пуассона. Эта формула выведена при важном допущении, что произведение np является постоянной величиной, т.е. 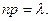 Тогда вероятность того, что событие А наступит ровно k раз, дается формулой, которая представляет собой закон распределения Пуассона вероятностей массовых и редких событий
Тогда вероятность того, что событие А наступит ровно k раз, дается формулой, которая представляет собой закон распределения Пуассона вероятностей массовых и редких событий
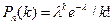 . (4)
. (4)
Пример: На базу отправлено 10000 изделий. Вероятность того, что изделие в пути получит повреждение, равна 0,0003. Найти вероятность того, что на базу прибудут 4 поврежденных изделия.
Решение. По условию задачи n=10000, p= 0,0003, k=4. находим 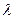 , а затем по формуле (11.4) и искомую вероятность.
, а затем по формуле (11.4) и искомую вероятность.
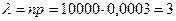 ,
, 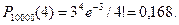
 2015-10-16
2015-10-16 363
363








