Задача 55

Дано уравнение эллипса .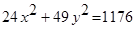

Найти:

1. длины его полуосей;

2. координаты фокусов;

3. эксцентриситет эллипса;

4. уравнения директрис и расстояния между ними;

5. точки эллипса, расстояние от которых до левого фокуса 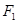равно 12.

Решение:

Запишем уравнение эллипса в каноническом виде: .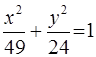

Отсюда 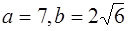. Используя соотношение 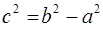, находим 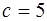. Следовательно, .

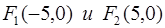По формуле 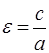найдем .

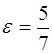Уравнения директрис 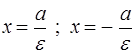имеют вид 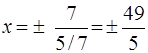, расстояние между ними .

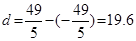По формуле 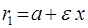находим абсциссу точек, расстояние от которых до точки 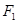равно 12:

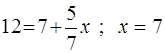. Подставляя значение x в уравнение эллипса, найдем ординаты этих точек: .

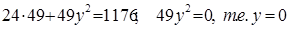Таким образом, условию задачи удовлетворяет точка A(7;0).