2015-10-13
705
Написать уравнение касательных к окружности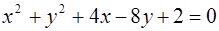 
, проходящих через начало координат.
Решение:
Уравнение касательной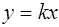 
, т.к. прямая проходит через начало координат.
Касательная к окружности имеет с ней одну общую точку. Чтобы найти эту точку, необходимо решить систему уравнений:
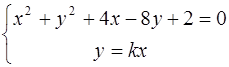
Подставляя второе уравнение в первое, получаем:
.
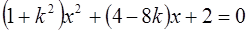Это уравнение имеет два равных корня, когда дискриминант равен нулю, т.е.
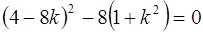
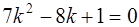
откуда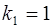 
, 
.
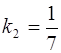Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек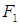 
и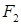 
есть величина постоянная (большая, чем расстояние между точкам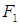и и 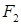). Координаты точек 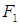и 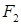, соответственно 
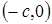и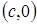 
.
Каноническое уравнение эллипса: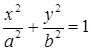 
.
Число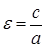 
называется эксцентриситетом эллипса.
Фокальными радиусами точки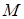 
эллипса называются отрезки прямых, соединяющие эту точку с фокусам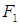и и 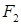. Их длины 
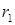и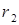 
задаются формулам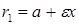и 
и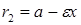 
. Прямые 
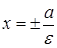называются директрисами эллипса. Директриса 
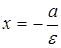называется левой, а 
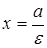‑ правой.
