Составить уравнение эллипса, проходящего через точки 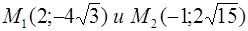 .
.
Решение:
Уравнение эллипса ищем в виде 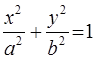 .
.
Так как эллипс проходит через точки 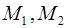 , то их координаты удовлетворяют уравнению эллипса:
, то их координаты удовлетворяют уравнению эллипса: 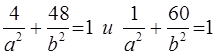 . Умножая второе равенство на (-4) и складывая с первым, находим
. Умножая второе равенство на (-4) и складывая с первым, находим 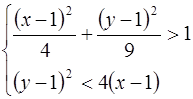 .
.
Подставляя найденное значение 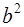 в первое уравнение, найдем
в первое уравнение, найдем 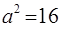 . Таким образом, искомое уравнение
. Таким образом, искомое уравнение 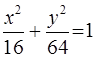 .
.
Задача 57.
Как расположены на плоскости точки, координаты которых удовлетворяют условиям:
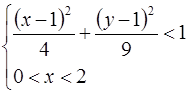 ;
; 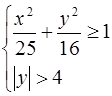 .
.
 2015-10-13
2015-10-13 389
389








