Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 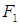 и
и 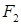 есть величина постоянная (не равная нулю и меньшая, чем расстояние между точками
есть величина постоянная (не равная нулю и меньшая, чем расстояние между точками 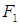 и
и 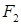 ).
).
Точки 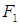 и
и 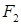 называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно
называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 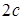 . Модуль расстояний от точек гиперболы до фокусов
. Модуль расстояний от точек гиперболы до фокусов 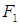 и
и 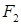 обозначим через
обозначим через 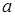 . По условию,
. По условию, 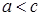 .
.
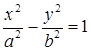 ,
,
где 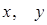 ‑ координаты произвольной точки гиперболы,
‑ координаты произвольной точки гиперболы,
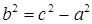 .
.
Уравнение 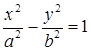 называется каноническим уравнением гиперболы.
называется каноническим уравнением гиперболы.
У гиперболы две асимптоты 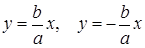 .
.
Эксцентриситетом гиперболы называется число 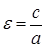 . Для любой гиперболы
. Для любой гиперболы 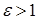 .
.
Фокальными радиусами точки гиперболы называются отрезки прямых, соединяющие эту точку с фокусами 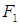 и
и 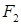 . Их длины
. Их длины 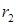 и
и 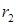 задаются формулами:
задаются формулами:
· Для правой ветви 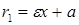 ,
,
· Для левой ветви 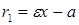 .
.
Прямые 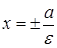 называются директрисами гиперболы. Как и в случае эллипса, точки гиперболы характеризуются соотношением
называются директрисами гиперболы. Как и в случае эллипса, точки гиперболы характеризуются соотношением 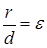 .
.
 2015-10-13
2015-10-13 317
317








