Далее везде будет обозначено: х(t) — входное воздействие; у(t) — выходная переменная звена.
1. Безынерционное звено описывается уравнением
y=kx, (4-1)
где k — коэффициент усиления звена.
Примерами такого звена являются (рис. 4-1): делитель напряжения (а), рычажная или редукторная передача (б, в), усилитель постоянного тока (г) и др. Предполагается, что передача сигнала от входа к выходу происходит мгновенно, без инерции. Очевидно, что передаточная функция звена имеет вид
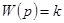 , (4-2)
, (4-2)
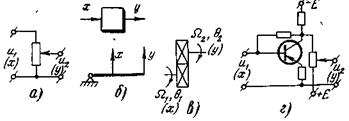
Рис 4-1 Примеры безынерционных звеньев
поэтому АФХ звена стянулась в точку (k,j 0) (рис. 4-2,а). Импульсная характеристика, находимая при подстановке 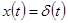 , равна
, равна 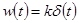 , а переходная функция
, а переходная функция 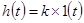 (рис. 4-2,6).
(рис. 4-2,6).
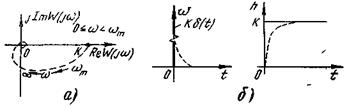
Рис 4-2 Динамические характеристики безынерционных звеньев
На практике даже рассмотренные на рис. 4-1 примеры не являются строго безынерционными звеньями. Так в делителе (рис. 4-1,а) не учитывается емкость и индуктивность между витками обмотки потенциометра и выходных, проводов, в рычажной передаче (рис. 4-1,б) не учитывается масса рычага, его упругость и т. д. Поэтому практически, например, переходная функция имеет вид пунктирной линии (рис. 4-2,б), т. е. выходная переменная не мгновенно следует за входной. Аналогично и АФХ имеет вид пунктирной линии (рис. 4-2,а) для частот ω>ωm. Однако в САР, работающих обычно в сравнительно низкочастотном диапазоне 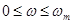 , инерционность рассмотренных устройств практически несущественна, поэтому их будем называть безынерционными. К таковым относится, помимо рассмотренных, большинство датчиков.
, инерционность рассмотренных устройств практически несущественна, поэтому их будем называть безынерционными. К таковым относится, помимо рассмотренных, большинство датчиков.
В ряде систем регулирования применяются устройства, работающие на несущей частоте (сельсины, усилители переменного тока с модуляцией и демодуляцией и др.). При частотах входного воздействия, много меньших несущей, эти устройства могут быть отнесены к безынерционным [2].
2. Инерционное звено описывается уравнением
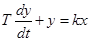 , (4-3)
, (4-3)
где k, Т — соответственно статический коэффициент усиления и постоянная времени звена.
Примеры инерционных звеньев: двигатель с линейной механической характеристикой (см. пример 3-2), термопара (пример 3-1). В качестве других примеров рассмотрим следующие.
Пример 4-1. RС -цепочка (рис. 4-3,а). Используя уравнение Кирхгофа, запишем
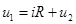 ,
, 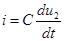 ,
,
поэтому 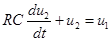 , что соответствует (4-3). Аналогично можно показать, что LR -цепочка (рис. 4-3,б) является инерционным звеном. С помощью операционных усилителей инерционное звено моделируется схемой рис. 4-3, г,
, что соответствует (4-3). Аналогично можно показать, что LR -цепочка (рис. 4-3,б) является инерционным звеном. С помощью операционных усилителей инерционное звено моделируется схемой рис. 4-3, г,
где Т=RС, 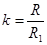 .
.
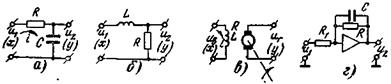
Рис 4-3 Примеры инерционных звеньев
Пример 4-2. Генератор постоянного тока с независимым возбуждением (рис. 4-3,в). Входное воздействие — напряжение возбуждения и в, приложенное к обмотке возбуждения
Генератора, имеющей индуктивность L и активное сопротивление R; выходная переменная — (э.д.с.) генератора и г. Для линеаризованного генератора (поскольку зависимость и г (i) имеет нелинейный характер из-за насыщения и гистерезиса) можно записать, опуская знак приращения,
и г =k 1 i. При этом 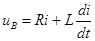 , поэтому
, поэтому
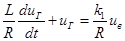
что соответствует уравнению инерционного звена (4-3), где постоянная времени 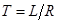 , а коэффициент усиления
, а коэффициент усиления 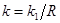 .
.
Рассмотрим другие динамические характеристики инерционного звена. Из (4-3) получаем выражение для передаточной функции
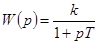 ,
, 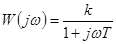 . (4-4)
. (4-4)
АФХ показана на рис. 4-4,а. Она имеет вид полуокружности, при этом на сопрягающей частоте 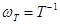 фазовый
фазовый
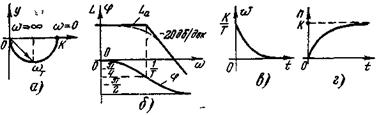
Рис. 4-4. Динамические характеристики инерционного звена
сдвиг равен 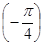 , а модуль равен
, а модуль равен 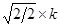 . Общее выражение для АЧХ и ФЧХ имеет вид
. Общее выражение для АЧХ и ФЧХ имеет вид
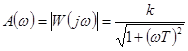 , (4-5а)
, (4-5а)
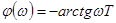 . (4-5б)
. (4-5б)
Построим логарифмические частотные характеристики.
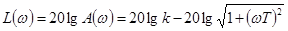 . (4-6а)
. (4-6а)
Эта зависимость показана на рис. 4-4,б пунктиром. Обычно применяют упрощенное построение ЛАЧХ, основанное на построении асимптот. Для инерционного звена точная характеристика заменяется двумя асимптотами: первая асимптота получается из (4-ба) при отбрасывании члена 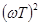 для частот
для частот 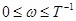 , а вторая — при отбрасывании единицы для частот
, а вторая — при отбрасывании единицы для частот 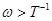 . Таким образом, асимптотическая ЛАЧХ записывается как
. Таким образом, асимптотическая ЛАЧХ записывается как
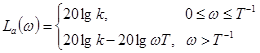 (4-6б)
(4-6б)
Легко заметить, что наклон второй асимптоты равен -20 дб/дек. Максимальная ошибка при использовании асимптотической ЛАЧХ (4-6б) вместо точной (4-6а) равна 3 дб и приходится на сопрягающую частоту. Эта ошибка практически исчезает на частотах, отличающихся от сопрягающей более чем в десять раз, т. е. при изменении частоты на 1 декаду. Заметим, кстати, что характеристика arctg ω T практически не отличается от своих крайних значений 0 и 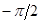 при изменении частот на 1 декаду от сопрягающей.
при изменении частот на 1 декаду от сопрягающей.
По теореме разложения (см. табл. 3) находим характеристики во временной области (рис. 4-4, в, г)
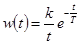 ,
, 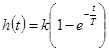 . (4-7)
. (4-7)
3. Интегрирующее звено описывается уравнениями
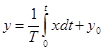
или
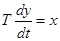
где Т — постоянная времени (коэффициент пропорциональности).
Пример 4-3. Примерами интегрирующих звеньев являются: электрическая емкость (рис. 4-5,а), индуктивность (б), вращающийся вал (в), гидравлический резервуар (г). Действительно, напряжение на емкости
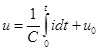 ,
,
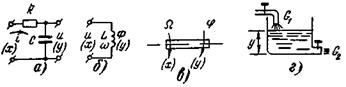
Рис 4-5 Примеры интегрирующих звеньев
магнитный поток в индуктивности, имеющей число вит ков w,
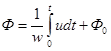 ,
,
угол поворота вала, вращающегося со скоростью Ω,
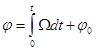 ,
,
уровень воды в цилиндрическом резервуаре сечения S
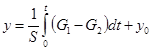 .
.
Передаточная функция интегрирующего звена легко находится из (4-8) по теореме о дифференцировании (или интегрировании при нулевых начальных условиях) оригинала (см. п. 5, 6 табл. 3-1):
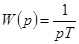 ,
, 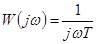 . (4-5)
. (4-5)
АФХ показана на рис. 4-6,а. Она имеет вид прямой, при этом фазовый сдвиг на всех частотах равен 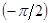 .
.
ЛАЧХ также имеет вид прямой с наклоном —20 дб/дек (рис. 4-6,б)
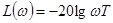 ,
, 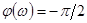 . (4-10)
. (4-10)
Временные динамические характеристики (рис. 4-6, г, д) записываются как
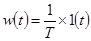 ,
, 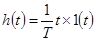 (4-11)
(4-11)
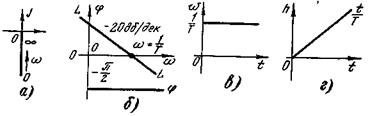
Рис 4-6 Динамические характеристики интегрирующего звена
4. Дифференцирующее звено (идеальное) описывается уравнением
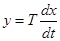 . (4-12)
. (4-12)
Пример 4-4. Примерами таких звеньев могут служить электрическая емкость (рис. 4-7,а), индуктивность (б), тахогенератор (ТГ) с постоянными магнитами (в). Действительно, ток в емкости
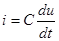
напряжение на индуктивности
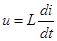
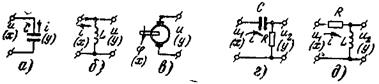
Рис. 4-7. Примеры идеальных и реальных дифференцирующих
напряжение ТГ постоянного тока
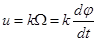 .
.
Надо заметить, что практически не существует реальных элементов, на выходе которых точно воспроизводилась бы производная от любого входного сигнала. Если бы это было так, то, подав на такой элемент скачкообразное входное воздействие, можно было бы получить на выходе δ-функцию, чего в реальных устройствах не бывает. Формальная запись для напряжений и токов в индуктивности и емкости (пример 4-4) не отражает законов коммутации электрических схем (напряжение на емкости и ток в индуктивности в реальных системах не могут измениться скачком). Аналогично нельзя, например, скачком изменить угол поворота вала реального ТГ, поскольку это потребовало бы бесконечно большого момента. Поэтому, хотя в структурных схемах применение идеальных дифференцирующих звеньев оправдано, практически они являются абстракциями. Реальное дифференцирующее звено описывается уравнением
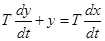 . (4-13)
. (4-13)
Это звено, имеющее передаточную функцию
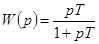 ,
, 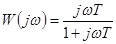 , (4-14)
, (4-14)
может быть представлено как последовательное соединение идеального дифференцирующего и инерционного звеньев.
Пример 4-5. Примерами таких звеньев являются СR- и LR - цепи (рис. 4-7, г, д), для которых можно записать:
для CR - цепи-
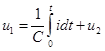 ,
,
где 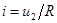 , поэтому после дифференцирования обеих частей исходного уравнения получаем
, поэтому после дифференцирования обеих частей исходного уравнения получаем
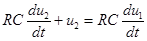 ;
;
для RL- цепи
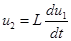 ,
,
где 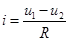 , поэтому
, поэтому
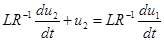 .
.
Из механических аналогов реального дифференцирующего звена следует назвать масляный катаракт, широко применяемый в механических САР (для авиационных, дизельных двигателей). АФХ реального дифференцирующего звена показана на рис. 4-8,а. Она имеет вид полуокружности,
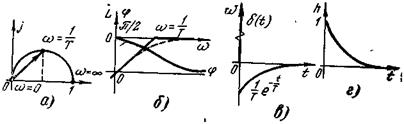
Рис. 4-8. Динамические характеристики реального дифференцирующего звена
причем на сопрягающей частоте коэффициент усиления звена равен 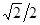 , а фазовый сдвиг
, а фазовый сдвиг 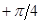 , хотя уже на больших частотах опережение по фазе практически исчезает. Тем не менее свойство дифференцирующих звеньев давать опережение по фазе широко используется при коррекции САР. Общее выражение для АЧХ и ФЧХ имеет вид
, хотя уже на больших частотах опережение по фазе практически исчезает. Тем не менее свойство дифференцирующих звеньев давать опережение по фазе широко используется при коррекции САР. Общее выражение для АЧХ и ФЧХ имеет вид
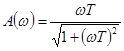 ,
, 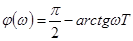
ЛАЧХ звена записывается как
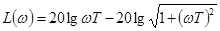
Построение асимптотической ЛАЧХ по этому выражению проводится, как и для инерционного звена, с помощью двух асимптот (рис. 4-8,б)
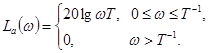 (4-15)
(4-15)
По теореме разложения (см. п. 9 табл. 3-1) находим характеристики во временной области (рис. 4-8, в, г)
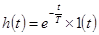 , (4-16а)
, (4-16а)
и после дифференцирования получаем (с учетом скачка переходной функции при t =0)
 . (4-16б)
. (4-16б)
5. Упругое (инерционно-форсирующее) звено описывается уравнением
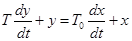 . (4-17)
. (4-17)
В зависимости от отношения 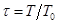 звено называют упругим интегрирующим (τ <1) или упругим дифференцирующим (τ >1), поскольку в первом случае оно дает, как показано ниже, отставание по фазе, а во втором — опережение. Передаточная функция звена имеет вид
звено называют упругим интегрирующим (τ <1) или упругим дифференцирующим (τ >1), поскольку в первом случае оно дает, как показано ниже, отставание по фазе, а во втором — опережение. Передаточная функция звена имеет вид
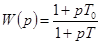 ,
, 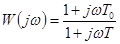 . (4-18)
. (4-18)
Пример 4-6 [2]. Рассмотрим RС - делители напряжения
по схеме рис. 4-9, а, б; получаем выражение для операторного коэффициента передачи
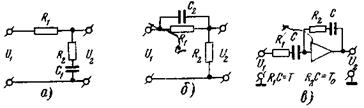
Рис 4-9. Примеры упругих звеньев
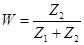 ,
,
где для схемы (а)
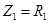 ,
, 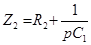 ,
,
а для схемы (б)
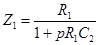
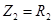 .
.
Поэтому схема (а) (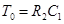 ,
, 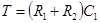 ) является упругим интегрирующим звеном, а схема (б) (
) является упругим интегрирующим звеном, а схема (б) (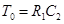 ,
, 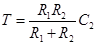 ) — упругим дифференцирующим. Такие звенья часто применяют при коррекции САР.
) — упругим дифференцирующим. Такие звенья часто применяют при коррекции САР.
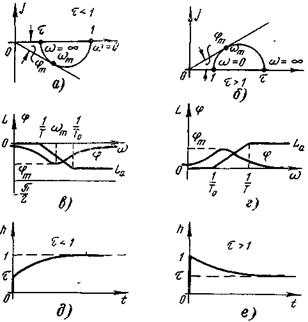
Рис. 4-10. Динамические характеристики упругих звеньев
АФХ для звена (4-18) показана на рис. 4-10, а, б, при этом
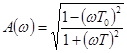 ,
, 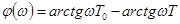 . (4-19)
. (4-19)
Из уравнения (4-19) легко найти частоту ωm, при которой фазовый сдвиг максимален по модулю: из условия 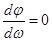 , получаем
, получаем
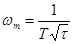 ,
, 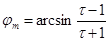 (4-20)
(4-20)
Асимптотические ЛАЧХ имеют вид (рис. 4-10, в, г): для τ <1
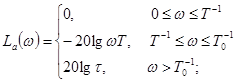
для τ >1
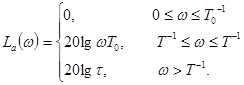
Переходную функцию (рис. 4-10, д, е) находим по теореме разложения
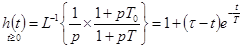 . (4-21)
. (4-21)
Импульсная характеристика содержит уже дельта-функцию, как и для дифференцирующего звена.
6. Колебательное звено описывается уравнением
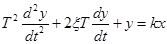 , (4-22)
, (4-22)
где k — статический коэффициент усиления, при степени затухания 0< ξ <1, что соответствует комплексным корням уравнения
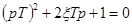 .
.
Заметим, что если корни последнего уравнения были бы действительными, то звено можно было бы представить виде двух последовательно соединенных инерционных (например, при ξ =1 получаем два инерционных звена одинаковыми постоянными времени Т).
Постоянная времени Т колебательного звена связана его резонансной частотой 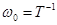 , поэтому иногда уравнение (4-22) записывают в виде
, поэтому иногда уравнение (4-22) записывают в виде
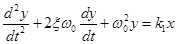 ,
, 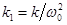 .
.
Пример 4-7. Примерами колебательных звеньев может быть RLC -контур (рис. 4-11, а) или упругая механическая система со значительной массой (б), простейшая следящая система с колебательным характером переходных процессов. Пример моделирования колебательного звена дан на рис. 4-11, в.
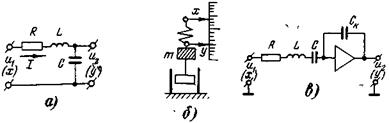
Рис. 4-11. Примеры колебательных звеньев
Для RLC -контура (а)
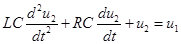 ,
,
поэтому при 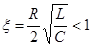 получаем (Колебательное звено с параметрами
получаем (Колебательное звено с параметрами 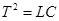 ,
, 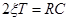 , k =1. Для механической (системы (рис. 4-11,б) уравнение.сил, действующих на тело массы т, имеет вид
, k =1. Для механической (системы (рис. 4-11,б) уравнение.сил, действующих на тело массы т, имеет вид
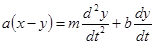 ,
,
где а, b — коэффициенты пружины и успокоителя.
Передаточная функция колебательного звена равна
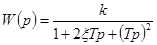 ,
, 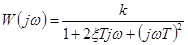 (4-24)
(4-24)
АФХ колебательного звена показана на рис. 4-12, а. Замечаем, что при 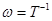 , когда
, когда 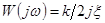 , фазовый сдвиг равен
, фазовый сдвиг равен 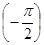 . С уменьшением степени затухания АФХ увеличивается в размерах (рис. 4-12,а), вырождаясь в две полупрямые при ξ = 0.
. С уменьшением степени затухания АФХ увеличивается в размерах (рис. 4-12,а), вырождаясь в две полупрямые при ξ = 0.
Асимптотическая ЛАЧХ (рис. 4-12,6) имеет вид
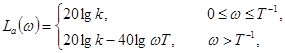 (4-25)
(4-25)
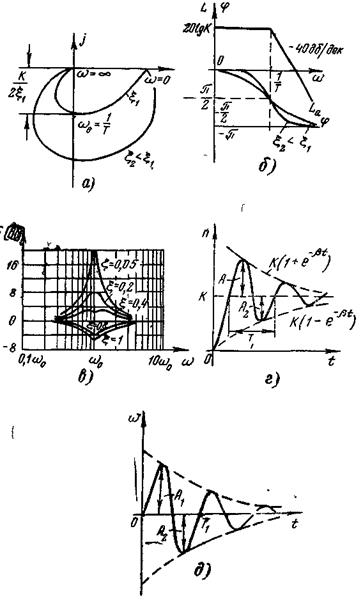
Рис. 4-12. Динамические характеристики колебательного звена
однако поправка к характеристике
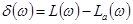
может достигнуть (в отличие от инерционного или реального дифференцирующего звеньев, где 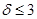 дб) сколь угодно большой величины при
дб) сколь угодно большой величины при 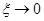 . Поэтому обычно график поправок (рис. 4-12,в) используют при построении ЛАЧХ. При 0,4< ξ <0,8 поправками можно не пользоваться. Чтобы воспользоваться теоремой разложения для нахождения импульсной характеристики и переходной функции, находим корни уравнения (4-23)
. Поэтому обычно график поправок (рис. 4-12,в) используют при построении ЛАЧХ. При 0,4< ξ <0,8 поправками можно не пользоваться. Чтобы воспользоваться теоремой разложения для нахождения импульсной характеристики и переходной функции, находим корни уравнения (4-23)
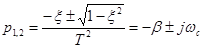 , (4-26)
, (4-26)
где  — коэффициент затухания;
— коэффициент затухания;
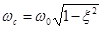 — собственная частота колебаний звена. Поэтому импульсная характеристика
— собственная частота колебаний звена. Поэтому импульсная характеристика
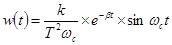 , (4-27)
, (4-27)
а переходная функция
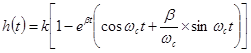 (4-28)
(4-28)
Графики этих характеристик показаны на рис. 4-12, г, д.
7. Звено запаздывания описывается уравнением
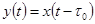 , (4-29)
, (4-29)
где τ 0 — время запаздывания.
Таким образом, выходная переменная звена повторяет входное воздействие, как и в безынерционном звене, но с запаздыванием. В автоматике звено запаздывания наиболее часто встречается в виде транспортного запаздывания (транспортировка твердых и сыпучих тел — по конвейерам и транспортерам, жидкостей — по трубопроводам, электроэнергии — по линиям электропередач и т. д.). По теореме запаздывания (см. табл. 3-1) из (4-29) получаем выражение для передаточной функции
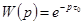 ,
, 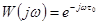 (4-30)
(4-30)
Учитывая, что  , получаем
, получаем
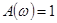 ,
, 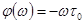 ,
,
АФХ и ЛАЧХ запаздывающего звена показана на рис. 4-13,а, 6.
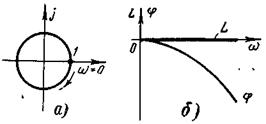
Рис 4-13 Частотные характеристики звена запаздывания
Другие типы звеньев подробно рассмотрены в [2].
 2015-10-13
2015-10-13 3395
3395
