Для удобства анализа САР, особенно имеющих несколько контуров, образованных за счет введения воздействий по возмущению, введения сигналов коррекции и т. д., необходимо уметь преобразовывать сложные структурные схемы в более простые. Теория преобразования структурных схем была разработана Б. Н. Петровым (1945 г.). При преобразовании структурной - схемы САР получаем новую схему, эквивалентную исходной только в отношении входных и выходных воздействий САР, т. е. не затронутых преобразованиями. Преобразование схем заключается в упрощающем схему переносе узлов и сумматоров, в получении схемы с неперекрещивающимися связями, когда отдельные контуры схемы не сцепляются друг с другом. После этого каждый контур заменяется одним звеном с эквивалентной передаточной функцией, и схема САР обычно приводится к типовой структуре (рис. 4-16) с приведен ными ко входу всеми воздействиями (задающим y 0, возмущающим f 0)
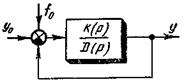
Рис. 4-16 Типовая структура САР
Перенос узлов или сумматоров может совпадать с направлением передачи сигнала (прямой перенос) или быть ему противоположен (обратный перенос). Основные правила структурных преобразований даны в табл. 4-1. Более подробные сведения о преобразованиях даны в[1, 2].
Таблица 4.1
| Преобразование | Исходная схема | Преобразованная схема | |
| Перенос сумматора через звено а)прямой б) обратный | 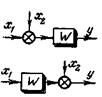 | 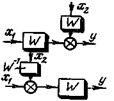 | |
| Перенос узла через звено а) прямой б) обратный | 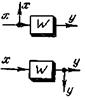 | 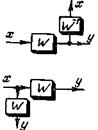 | |
| 3 | Перенос узла или сумматора по разветвленной цепи | 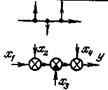 | 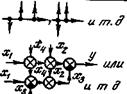 |
Рис 4* Правила структурных преобразований
Пример 4-9. Рассмотрим САР скорости двигателя с компенсацией возмущений нагрузки. Схема системы дана на рис. 1-8 (см. пример 1-3). Функциональная схема такой САР дана на рис. 4-17, а. Объектом регулирования является двигатель, при этом регулируемая величина — скорость двигателя W определяется измерительным устройством (тахогенератором) и сравнивается с уставкой. Ошибка в виде напряжения Δ U поступает на усилительное устройство (электромашинный усилитель), напряжение на выходе которого является управляющим для двигателя. Скорости последнего зависит также от момента нагрузки М н, которая измеряется и с целью компенсации поступает также на вход усилительного устройства. Таким образом, здесь, реализуется принцип двухканальности Б. Н. Петрова как необходимое условие получения инвариантной к возмущению нагрузки САР. Структурная схема САР, включающая в себя звенья направленного действия с одним входом и выходом, сумматоры, узлы и связи, показана на рис. 4-17,6, где обозначено:
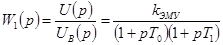 передаточная функция ЭМУ;
передаточная функция ЭМУ;
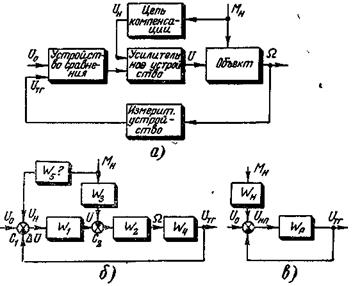
Рис. 4-17. Функциональная и структурная схемы САР скорости двигателя
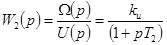 передаточная функция двигателя по каналу «напряжение — скорость»;
передаточная функция двигателя по каналу «напряжение — скорость»;
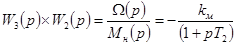 передаточная функция двигателя по каналу «момент нагрузки — скорость»;
передаточная функция двигателя по каналу «момент нагрузки — скорость»;
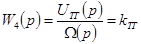 передаточная функция тахогенератора;
передаточная функция тахогенератора;
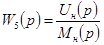 — неизвестная пока передаточная функция цепи компенсации, которую необходимо найти из условия инвариантности САР к возмущению нагрузки.
— неизвестная пока передаточная функция цепи компенсации, которую необходимо найти из условия инвариантности САР к возмущению нагрузки.
Замечание. Передаточная функция двигателя и структурное изображение двигателя в виде двух звеньев и сумматора С 2 на рис. 4-17, б соответствует уравнению двигателя (3-9), при этом знак минус в (3-9) отнесен к сумматору.
Для нахождения W 5 преобразуем структурную схему, перенеся сумматор С 2 через звено W 1и объединяя сумматоры (см. п. 1б, п. 3 табл. 4-1), что соответствует приведению возмущения к одной точке приложения на входе системы в виде некоторого эквивалентного приведенного напряжения нагрузки U нп (рис. 4-1 7,в). При этом последовательно соединенные звенья заменяются одним звеном с передаточной функцией 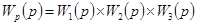 , а для параллельно соединенных звеньев получаем
, а для параллельно соединенных звеньев получаем 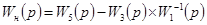 . Очевидно, САР будет абсолютно инвариантной к возмущению нагрузки, если обеспечить
. Очевидно, САР будет абсолютно инвариантной к возмущению нагрузки, если обеспечить 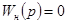 , откуда получаем искомую передаточную функцию
, откуда получаем искомую передаточную функцию
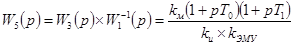 .
.
К сожалению, точная реализация передаточных функций, имеющих более высокий порядок полинома от р в числителе, чем в знаменателе, невозможна. Это связано, как указывалось при обсуждении свойств идеального дифференцирующего звена (см. пример 4-4), с невозможностью получения таких звеньев. Однако, введя небольшие инерционности в 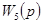 , легко можно реализовать передаточную функцию
, легко можно реализовать передаточную функцию
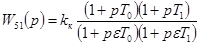 ,
, 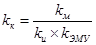 ,
,
где ε - малая величина, например, 5 %.
Понятно, что полученная в этом случае САР не будет абсолютно инвариантной, а лишь инвариантной до ε, т. е. в переходных режимах действие нагрузки будет проявляться, но весьма малым образом.
Заметим, что в лабораторной работе, где исследуется такая САР, цепь компенсации взята безынерционной в виде 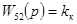 причем коэффициент
причем коэффициент 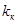 подбирается экспериментально перемещением движка потенциометра П 2 (см. рис. 1-8). Такая цепь компенсации обеспечивает инвариантность САР к М н лишь в установившихся режимах, что легко проверить экспериментально, давая скачкообразные изменения нагрузки при коммутации ключа К 1.
подбирается экспериментально перемещением движка потенциометра П 2 (см. рис. 1-8). Такая цепь компенсации обеспечивает инвариантность САР к М н лишь в установившихся режимах, что легко проверить экспериментально, давая скачкообразные изменения нагрузки при коммутации ключа К 1.
Пример 4-10. Рассмотрим комбинированную следящую систему, структурная схема которой показана на рис. 4-18, а, в которой для улучшения ее динамических свойств введена цепь с неизвестной пока передаточной функцией 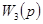 , которую найдем из условия идеальной следящей системы, когда
, которую найдем из условия идеальной следящей системы, когда 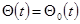 , т. е. передаточная функция следящей системы
, т. е. передаточная функция следящей системы 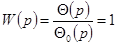 . Перенося сумматор на вход системы (рис. 4-18, б), получим
. Перенося сумматор на вход системы (рис. 4-18, б), получим
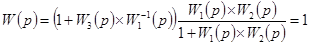 .
.
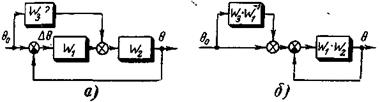
Рис. 4-18 Структурная схема комбинированной следящей системы
Таким образом, искомая цепь должна иметь передаточную функцию 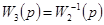 . Поскольку
. Поскольку 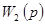 соответствует двигателю, то точная реализация такой цепи также затруднена из-за трудностей получения дифференцирующих устройств. Улучшения свойств следящей системы, как и в предыдущем примере, все-таки можно было бы добиться, приближенно реализуя
соответствует двигателю, то точная реализация такой цепи также затруднена из-за трудностей получения дифференцирующих устройств. Улучшения свойств следящей системы, как и в предыдущем примере, все-таки можно было бы добиться, приближенно реализуя 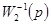 .
.
Основной проблемой при создании комбинированных систем является проблема датчиков возмущающих, а иногда и задающих воздействий.
Глава 5
 2015-10-13
2015-10-13 1140
1140
