Распределение Пуассона

Распределение Пуассона является предельным для биноминаль­ного распределения, когда вероятность (q £ 0,1) мала, число собы­тий велико, а математическое ожидание 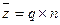появления дефек­тных изделий является ограниченным числом.

Это распределение часто называют законом распределения редких событий. При таких условиях формула

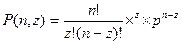
заменяется на формулу

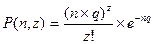
причем

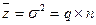
Таблица 12.4

Сопоставление распределений

Число дефектных изделий z	Вероятность биноминального распределения P(n;z)	Вероятность распределения Пуассона
q = 0,5; n = 6	q = 0,1; n = 30	q = 0,05; п = 60	q = 0,01; n = 300
	0,0156	0,0424	0,0461	0,0490	0,0498
	0,3125	0,2361	0,2298	0,2252	0,2240
		0,004	0,0006	0,0008	0,008

Глава 13.

Выборочный приемочный контроль

И качество измерений