Объем тела вращения

Пусть вокруг оси ОХ вращается криволинейная трапеция, ограниченная осью ОX, прямыми x=a и x=b и кривой 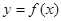, где 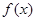- непрерывная, неотрицательная на отрезке [a; b] функция. Тогда эта криволинейная трапеция опишет тело, являющееся телом вращения.

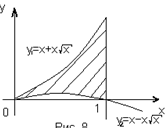
Пример 8. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной двумя ветвями кривой 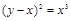и прямой х=1.

Решение:

искомый объем получается как разность двух объемов, получающихся при вращении вокруг оси ОХ двух криволинейных трапеций, ограниченных сверху соответственно кривым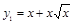и и 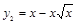. Область определения функции

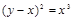
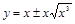
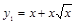
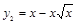
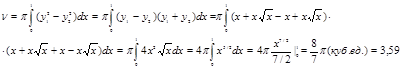
Вычисление длины дуги