2.1.I.Площадь в прямоугольных декартовых координатах Площадь криволинейной трапеции
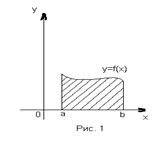 При постановке задачи определенного интегрирования мы уже рассмотрели вопрос о вычислении площади криволинейной трапеции, т.е. фигуры, ограниченной прямыми x=a, x=b, y=0 и кривой y=f(x), гдеf(x) - неотрицательная, непрерывная на отрезке [a;b] функция, и установили, что площадь указанной фигуры вычисляется по формуле
При постановке задачи определенного интегрирования мы уже рассмотрели вопрос о вычислении площади криволинейной трапеции, т.е. фигуры, ограниченной прямыми x=a, x=b, y=0 и кривой y=f(x), гдеf(x) - неотрицательная, непрерывная на отрезке [a;b] функция, и установили, что площадь указанной фигуры вычисляется по формуле 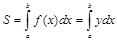 (рис. 1)
(рис. 1)
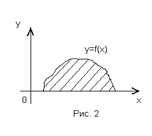
 Если криволинейная трапеция ограничена.осью ОХ и другой кривой y= f(x), где f(x) - непрерывная, неотрицательная на данном отрезке функция, то для вычисления площади такой фигуры надо предварительно найти абсциссы точек пересечения кривой с осью OX, затем применить формулу (I) (рис. 2).
Если криволинейная трапеция ограничена.осью ОХ и другой кривой y= f(x), где f(x) - непрерывная, неотрицательная на данном отрезке функция, то для вычисления площади такой фигуры надо предварительно найти абсциссы точек пересечения кривой с осью OX, затем применить формулу (I) (рис. 2).
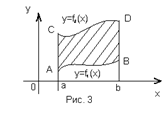
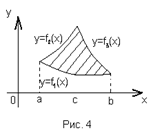 Если плоская фигура ограничена и снизу и сверху кривыми, уравнения которых y=f1(x) и y=f2(x), где a≤x≤b и функции f1(x), f2(x) – непрерывны причём f1(x)≤ f2(x), искомая площадь будет представлять собой разность площадей криволинейных трапеций aABb и aCDb:
Если плоская фигура ограничена и снизу и сверху кривыми, уравнения которых y=f1(x) и y=f2(x), где a≤x≤b и функции f1(x), f2(x) – непрерывны причём f1(x)≤ f2(x), искомая площадь будет представлять собой разность площадей криволинейных трапеций aABb и aCDb:
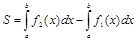 или
или 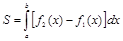 (рис. 3).
(рис. 3).
Пусть фигура ограничена сверху или
снизу дугами нескольких кривых. Для вычисления площади такой фигуры стараются разбить эту фигуру на части прямыми, параллельными оси Оу, так, чтобы каждая часть была ограничена только одной кривой, как сверху, так и снизу.
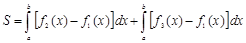
(для случая, указанного на рис. 4).
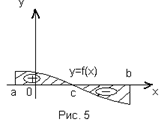 Если непрерывная на [a;b] функция f(x) меняет на нем знак так, что некоторые части графика данной функции находятся с одной стороны от оси ОХ, а иные - с другой, то для вычисления площади фигуры поступим следующим образом: в отдельности вычисляют площадь фигуры, расположенной выше оси ОХ, и фигуры ниже оси ОХ.
Если непрерывная на [a;b] функция f(x) меняет на нем знак так, что некоторые части графика данной функции находятся с одной стороны от оси ОХ, а иные - с другой, то для вычисления площади фигуры поступим следующим образом: в отдельности вычисляют площадь фигуры, расположенной выше оси ОХ, и фигуры ниже оси ОХ.
А затем берут сумму абсолютных величин всех полученных интегралов.
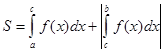 .
.
Пример 7. Вычислить площадь фигуры, ограниченной осью ОХ и синусоидой 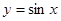 при 0≤х≤2π.
при 0≤х≤2π.
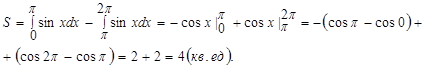
 2015-10-13
2015-10-13 653
653








