Пусть в полярной системе координат дана кривая, уравнение которой 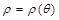 , где
, где 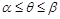 . Функция
. Функция 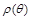 имеет непрерывную производную на сегменте
имеет непрерывную производную на сегменте 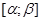
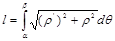 .
.
Пример 11. Найти всю длину кривой 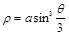 .
.
Решение: 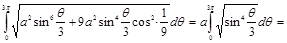
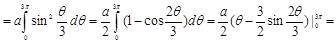
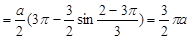 .
.
Здесь имеем 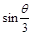 при
при 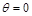 и при
и при 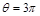 .
.
Площадь поверхности вращения
Требуется вычислить площадь поверхности, образованной вращением кривой y= f (x), где f (x) – непрерывная на 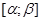 функция, вокруг оси ОХ.
функция, вокруг оси ОХ.
Пусть функция f (x) имеет непрерывную производную 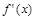 на отрезке
на отрезке 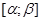
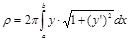 .
.
Если дуга АВ задана параметрическими уравнениями, то
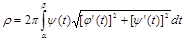 .
.
Пример 12. Определить площадь поверхности, образованной вращением вокруг оси ОХ дуги кривой 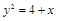 , отсеченной прямой х=2.
, отсеченной прямой х=2.
Решение: 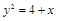 ,
, 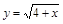 :
: 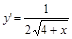
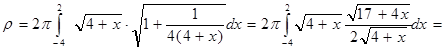
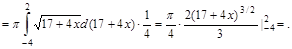
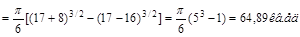
 2015-10-13
2015-10-13 726
726








