1.15. Как должны быть согласованы размеры матриц-множителей, чтобы операция умножения была определена? Матрица какого размера при этом получается?
 1.16. Сформулируйте определение произведения матриц.
1.16. Сформулируйте определение произведения матриц.
1.17. Даны матрицы: 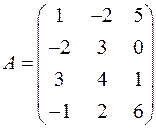 и
и 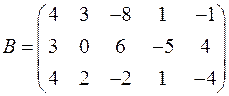 . Найдите следующие элементы матрицы
. Найдите следующие элементы матрицы 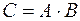 :
: 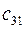 ;
; 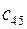 ;
; 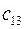 .
.
1.18. Выполните действия:
а) 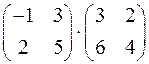 ; б)
; б) 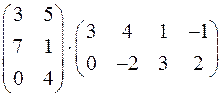 ;
;
в) 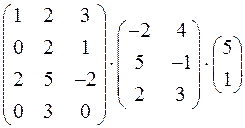 .
.
1.19. Даны матрицы 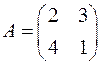 и
и 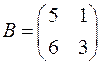 . Найти произведения:
. Найти произведения: 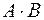 и
и 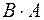 . Обладает ли операция умножения матриц свойством коммутативности? Как называют матрицы, для которых имеет место коммутативность умножения?
. Обладает ли операция умножения матриц свойством коммутативности? Как называют матрицы, для которых имеет место коммутативность умножения?
1.20. Найдите все матрицы, перестановочные с данной:
а) 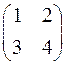 ; б)
; б) 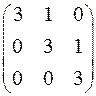 .
.
1.21. Выполните действие: 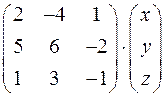 .
.
1.22. Используя операцию умножения матриц, запишите систему уравнений 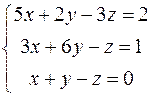 в виде матричного равенства.
в виде матричного равенства.
1.23. Пусть 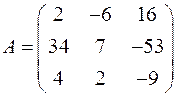 . Найдите произведения
. Найдите произведения 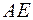 и е
и е 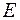 - единичная матрица соответствующего размера. Сделайте выводы.
- единичная матрица соответствующего размера. Сделайте выводы.
1.24*. Докажите, что умножение матриц а) ассоциативно; б) дистрибутивно относительно сложения.
1.25. Какого размера должна быть матрица, чтобы ее можно было умножить саму на себя?
1.26. Как определяется натуральная степень квадратной матрицы?
1.27. Выполните действия:
а) 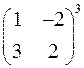 ; б)
; б) 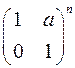 ,
,  ; в)
; в) 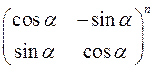 .
.
1.28*. Найдите все матрицы 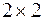 , квадраты которых равны нулевой матрице.
, квадраты которых равны нулевой матрице.
1.29*. Найдите все матрицы 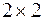 , квадраты которых равны единичной матрице.
, квадраты которых равны единичной матрице.
1.30. Найдите значение многочлена 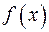 от матрицы
от матрицы 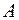 :
:
а) 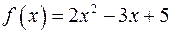 ,
, 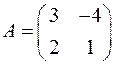 ;
;
б) 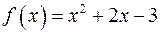 ,
, 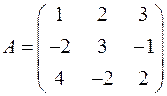 .
.
 2015-10-13
2015-10-13 355
355








