Разработка прогнозов методом наименьших квадратов

Сущность метода состоит в минимизации суммы квадратических отклонений между наблюдаемыми и расчетными величинами. Расчетные величины находятся по подобранному уравнению – уравнению регрессии.

Чем меньше расстояние между фактическими значениями и расчетными, тем более точен прогноз, построенный на основе уравнения регрессии. Теоретический анализ сущности изучаемого явления, изменение которого отображается временным рядом, служит основой для выбора кривой. Иногда принимаются во внимание соображения о характере роста уровней ряда. Так, если рост выпуска продукции ожидается в арифметической прогрессии, то сглаживание производится по прямой. Если же оказывается, что рост идет в геометрической прогрессии, то сглаживание надо производить по показательной функции.

Рабочая формула метода наименьших квадратов:

у _t₊₁ = а×Х + b, (4)

где t + 1 – прогнозный период;

y_t₊₁ – прогнозируемый показатель;

a и b - коэффициенты;

Х - условное обозначение времени.

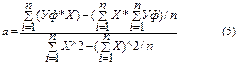Расчет коэффициентов a и b осуществляется по следующим формулам:

где, Уф – фактические значения ряда динамики;

n – число уровней временного ряда;

Сглаживание временных рядов методом наименьших квадратов служит для отражения закономерности развития изучаемого явления. В аналитическом выражении тренда время рассматривается как независимая переменная, а уровни ряда выступают как функция этой независимой переменной. Ясно, что развитие явления зависит не от того, сколько лет прошло с отправного момента, а от того, какие факторы влияли на его развитие, в каком направлении и с какой интенсивностью. Развитие явления во времени выступает как результат действия этих факторов.

Правильно установить тип кривой, тип аналитической зависимости от времени – одна из самых трудных задач предпрогнозного анализа.

Подбор вида функции, описывающей тренд, параметры которой определяются методом наименьших квадратов, производится в большинстве случаев эмпирически, путем построения ряда функций и сравнения их между собой по величине среднеквадратической ошибки, вычисляемой по формуле

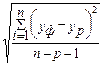S = , (7)

где y_ф – фактические значения ряда динамики;

y_р – расчетные (сглаженные) значения ряда динамики;

n – число уровней временного ряда;

р – число параметров, определяемых в формулах, описывающих тренд.

Недостатки метода наименьших квадратов:

1) изучаемое экономическое явление мы пытаемся описать с помощью математического уравнения, поэтому прогноз будет точен для небольшого периода времени, и уравнение регрессии следует пересчитывать по мере поступления новой информации;

2) сложность подбора уравнения регрессии. Эта проблема разрешима при использовании типовых компьютерных программ.

Определим прогнозное значение валовой продукции растениеводства на 2010-2011 гг., используя метод наименьших квадратов

Для решения используем следующие табличные значения

Годы	ВП растениеводства, тыс. руб. Уф	Условное обо-значение времени Х	Уф*Х	Х^2	Ур	Расчет средней относительной ошибки / Уф - Ур/ Уф * 100

	19,6 101,0 171,5 348,6 493,2 610,7 701,3 875,4		19,6 202,0 514,5 1394,4 2466,0 3664,2 4909,1 7003,2		-20,6 103,9 228,4 352,9 477,4 601,9 726,4 850,9	2,05 2,87 33,17 1,23 3,20 1,44 3,58 2,8
Итого	3321,3					50,32
прогноз	975,4 1099,9