Примеры выполнения практических задании

Задача 1.

С какой вероятностью можно утверждать, что гипотеза о равенстве математических ожиданий емкости конденсаторов двух партий верна, если известны

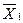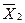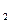средние значения емкости в выборках: =9880 пФ, =10100 пФ. Среднее квадратическое отклонение емкости одинаково и равно 500 пФ. Объемы выборок n =30, n =25.

Решение.

Выдвигаем конкурирующую гипотезу Н :M[X ]≠M[X₂].Вычислим наблюдаемое значение Z-критерия по формуле (11):

.

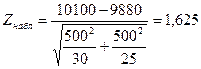По вычисленному значению Z =1,625 и по табл. П2 находим значение функции Лапласа Ф(Z)=0,4495. Зная, что Ф(Z)=0,5P, находим вероятность того, что емкость конденсаторов в двух партиях одинакова Р=2Ф(Z)=0.899.

Ответ: вероятность того, что емкость конденсаторов в двух партиях одинакова равна 0,899.

и сравнить с табличным значением Z 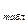найденным по табл. П2 функции Лапласа из равенства Ф(Z 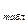)= 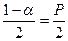для конкурирующей гипотезы H :М[Х ] ≠ М[Х ].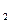

Если конкурирующая гипотеза имеет вид:

Н : М[ X ] > М[ Х₂ ] или Н : М[ X ] < М[ Х₂ ],

то в этих случаях табличное значение Z 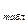находят по таблице функции Лапласа

по формуле: .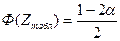

Если 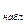| Z |< Z 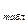, то нет оснований отвергнуть нулевую гипотезу Н .

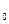Если 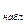| Z |> Z 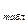, нулевую гипотезу отвергают.

Проверка гипотезы о равенстве средних, дисперсии которых неизвестны осуществляется с использованием критерия Стьюдента.

Для проверки нулевой гипотезы H_Q: M[X ]=M[X₂] при заданном уровне значимости надо вычислить наблюдаемое значение t-критерия t _набл. по формуле

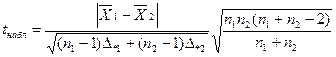, (12)

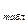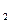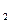сравнить с табличным значением t , найденным по таблице распределения Стьюдента (табл. ПЗ) по уровню значимости (вдвое заданного при конкурирующей гипотезе H :М[Х ] ≠ М[Х ] и числу степеней свободы K= n +n -2.

При конкурирующих гипотезах вида Н :М[X ]> М[ Х₂] или Н :М[X ] <М[Х₂ ] табличное значение t _табл. находят по уровню значимости.

Если 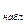| t |< t 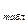, то нет оснований отвергнуть нулевую гипотезу Н .

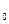Если 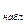| t |> t 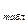, тонулевую гипотезу отвергают.