При сравнительном анализе конструкций или технологических процессов производства РЭС по точности и стабильности на основе выборочных данных возникает задача проверки статистических гипотез. Под статистически понимаются такие гипотезы, в которых проверяются предположения, выдвину относительно каких-либо параметров закона распределения случайной величины, или относительно вида закона распределения случайной величины. Наибольшее применение в решении технических задач находят методы проверки статистических гипотез первого вида. При этом предполагается, что вид закона распределения сравниваемых величин одинаков, и особенности закона распределения каждой них заключаются в различиях значений параметров (математического ожидания, дисперсии). Эти различия отражают изменения в показателях качества конструкции
или технологических процессов. Эти методы являются основой выборочного текущего и приемочного контроля качества продукции.
Рассмотрим, например, применение этих методов в текущем контроле стабильности технологического процесса производства резисторов. Пусть случайная
величина X - значение сопротивления конкретного резистора, 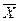 - выборочное среднее, определенное по результатам выборки объема п,
- выборочное среднее, определенное по результатам выборки объема п, 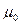 - требуемое номинальное значение сопротивления резистора, μ - неизвестное нам генеральное среднее в данной контролируемой партии резисторов.
- требуемое номинальное значение сопротивления резистора, μ - неизвестное нам генеральное среднее в данной контролируемой партии резисторов.
Задача заключается в том, чтобы установить, соответствуют ли изготавливаемые резисторы требуемому номинальному значению сопротивления, т, е. необходимо
определить, можно ли считать, что μ = 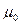 , проверяя при этом не всю партию, а выборку объемом п. Вследствие разных причин, например, нарушений технологического процесса, низкого качества сырья генеральное среднее μ
, проверяя при этом не всю партию, а выборку объемом п. Вследствие разных причин, например, нарушений технологического процесса, низкого качества сырья генеральное среднее μ
контролируемой партии может быть и не равно 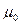 . Если вычисленное по выборке
. Если вычисленное по выборке
X незначительно отличается от 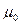 , то предположение о совпадении μ и
, то предположение о совпадении μ и 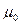 можно считать оправданным. Необходимо установить, насколько велика может
можно считать оправданным. Необходимо установить, насколько велика может
быть разности. (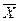 —
— 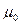 ), чтобы гипотеза о совпадении μ и
), чтобы гипотеза о совпадении μ и 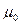 была отвергнута
была отвергнута
как ложная. Предположим, что M[ 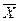 ]= μ =
]= μ = 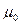 , назовем эту гипотезу нулевой и обозначим ее Н0, тогда наше предположение можно записать так: Н
, назовем эту гипотезу нулевой и обозначим ее Н0, тогда наше предположение можно записать так: Н 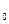 : μ =
: μ = 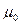 .
.
Если гипотеза Н0 верна, то M  [
[ 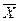 ]=
]= 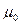 ,, и плотность распределения выборочного среднего f(x) имеет вид, показанный на рис. 7. Если гипотеза Н0 не верна, и в действительности μ >
,, и плотность распределения выборочного среднего f(x) имеет вид, показанный на рис. 7. Если гипотеза Н0 не верна, и в действительности μ > 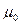 , т. е. верна так называемая конкурирующая гипотеза
, т. е. верна так называемая конкурирующая гипотеза
Н  : μ >
: μ > 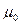 , то плотность распределения выборочного среднего
, то плотность распределения выборочного среднего 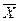 будет расположена правее f(x), представленной на рис. 7.
будет расположена правее f(x), представленной на рис. 7.

F(x) область принятия гипотезы область непринятия гипотезы
α
Рис.7. 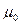
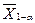
По таблице F - распределения (табл. П5) находим Fтабл по заданному уровню значимости α и числам степеней свободы К  и К2 (К
и К2 (К  - число степеней свободы, большой исправленной выборочной дисперсии).
- число степеней свободы, большой исправленной выборочной дисперсии).
Если F 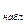 < F
< F 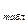 , то нет оснований отвергнуть нулевую гипотезу.
, то нет оснований отвергнуть нулевую гипотезу.
Если F 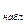 >F
>F 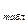 , тонулевую гипотезу отвергают.
, тонулевую гипотезу отвергают.
Если необходимо сравнить несколько дисперсий с определенным уровнем значимости α, то поступают следующим образом. В каждой из l серий измерений осуществляемых, например, различными приборами, проводят одинаковое количество опытов п или берут из них выборки одинакового объема. Вычисляют: число степеней свободы К. Для каждой серии по (3) подсчитывают эмпирические
дисперсии 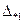 ,
, 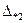 ,…,
,…, 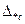 ,…,
,…, 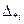 (i =1,2,…, l;
(i =1,2,…, l; 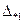 >
> 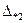 ). Далее наибольшую по абсолютной величине эмпирическую дисперсию
). Далее наибольшую по абсолютной величине эмпирическую дисперсию 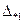 сравнивают с суммой всех дисперсий по критерию Кохрена:
сравнивают с суммой всех дисперсий по критерию Кохрена:
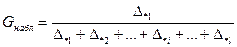 . (14)
. (14)
Задаваясь требуемым уровнем значимости в зависимости от l и К по табл.П6 находят критическое значение G-критерия.
Если G 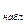 <G
<G 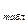 , то нет оснований отвергнуть нулевую гипотезу.
, то нет оснований отвергнуть нулевую гипотезу.
Если G 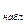 >G
>G 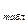 , тонулевую гипотезу отвергают.
, тонулевую гипотезу отвергают.
 2015-10-13
2015-10-13 366
366








