Интервальное оценивание особенно необходимо при малом объеме выбора когда точечная оценка в значительной мере случайна.
Интервальной называют оценку, которая определяется двумя числами - концами интервала, покрывающими оцениваемый параметр. В качестве границ доверительного интервала принимаются такие случайные величины, при которых
вероятность того, что истинное значение параметра Θ окажется внутри этого
интервала, близка к единице. Эту вероятность называют доверительной и е
берут равной 0,9; 0,95; 0,99. Величину α.=1-р называют уровнем значимости
или вероятностью ошибки.
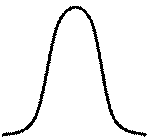
Принцип интервальной оценки поясняется на рис. 2.(а,б).


 F(Θ)
F(Θ)
а)

Θ
 |

 f(Θ) Θ
f(Θ) Θ 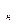 Θ
Θ 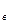
б)
Θ 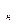 Θ
Θ 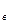 Θ
Θ
Рис. 2.
Здесь F(Θ) и f(Θ), соответственно, интегральная функция и плотность распределения оценки Θ. Площадь под кривой f(Θ), заключенная между
верхней Θ 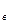 и нижней Θ
и нижней Θ 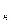 границами доверительного интервала, равна выбранному значению доверительной вероятности, т. е. вероятности того, что найденный доверительный интервал покрывает неизвестное нам истинное значение параметра. Сумма заштрихованных площадок равна уровню значимости α.
границами доверительного интервала, равна выбранному значению доверительной вероятности, т. е. вероятности того, что найденный доверительный интервал покрывает неизвестное нам истинное значение параметра. Сумма заштрихованных площадок равна уровню значимости α.
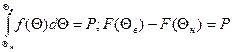 .
.
На рис.2 изображен двухсторонний доверительный интервал [ Θ 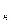 ;Θ
;Θ 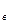 ], относительно которого с заранее выбранной вероятностью Р можно сказать, что внутри этого интервала находится истинное значение параметра, т. е.
], относительно которого с заранее выбранной вероятностью Р можно сказать, что внутри этого интервала находится истинное значение параметра, т. е.
Р{ Θ 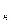 < Θ < Θ
< Θ < Θ 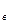 }=P=1-α.
}=P=1-α.
Во многих случаях целесообразно находить односторонний доверительный интервал: верхний или нижний, которые задаются в общем случае выражениями:
Р{ Θ 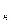 < Θ}=P; Р{Θ< Θ
< Θ}=P; Р{Θ< Θ 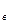 }=P.
}=P.
Принцип построения односторонних доверительных интервалов аналогичен изображенному на рис. 2, но заштрихованная площадка, равная α, располагается с одной стороны под кривой плотности распределения.
Функции доверительного интервала случайны, т. е. находятся по выборочным данным. Чем больше объем выборки, тем уже доверительный интервал для той же доверительной вероятности Р. Чем больше выбранная вероятность, тем шире для той же самой выборки доверительный интервал.
Таким образом, зная выборочное распределение оценки, можно определить
границы доверительного интервала Θ 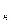 и. Θ
и. Θ 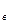 для выбранной доверительной вероятности Р.
для выбранной доверительной вероятности Р.
В математической статистике наиболее полно получены выборочные распределения оценок математического ожидания и дисперсии для нормально распределенной величины X. При этом выборочное распределение оценки X при известной генеральной дисперсии (σ2 является также нормальным, и поэтому доверительные интервалы здесь находятся с использованием нормального распределения.
Доверительный интервал для математического ожидания при известной дисперсии σ2 генеральной совокупности
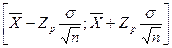 , (7)
, (7)
где σ – среднеквадратическое отклонение генеральной совокупности;
Критические значения х 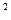 при надежности и числе степеней свободы К.
при надежности и числе степеней свободы К.
Таблица П4.
| к | |||||||||
| 0.8 | 0.9 | 0.95 | 0.98 | 0.99 | 0.995 | 0.998 | 0.999 | ||
| 5.99 | 7.78 | 9.49 | 11.67 | 13.28 | 14.9 | 16.9 | 18.5 | ||
| 7.29 | 9.24 | 11.07 | 13.39 | 15.09 | 16.3 | 18.9 | 20.5 | ||
| 8.56 | 10.64 | 12,59 | 15.03 | 16.8 | 18.6 | 20.7 | 22.5 | ||
| 9.8 | 12.02 | 14.07 | 16.6 | 18.5 | 20.3 | 22.6 | 24.3 | ||
| 11.03 | 13.36 | 15.51 | 18.2 | 20.1 | 21.9 | 24.3 | 26.1 | ||
| 12.24 | 14.68 | 16.9 | 19.7 | 21.7 | 23.6 | 26.1 | 27.9 | ||
| 13.44 | 15.99 | 18.3 | 21.2 | 23.2 | 25.2 | 27.7 | 29.6 | ||
| 1! | 14.63 | 17.3 | 19.7 | 22.6 | . 24.7 | 26.8 | 29.4 | 31.3 | |
| 15.8 | 18.5 | 24.1 | 26.2, | 28.3 | 32.9 | ||||
| 19.8 | 22.4 | 25.5 | 27.7 | 29.8 | 32.5 | 34.5 | |||
| 18.2 | 21.1 | 23.7 | 26.9 | 29.1 | 31.3 | 36.1 | |||
| 19.3 | 22.3 | 28.3 | 30.6 | 32.7 | 35.6 | 37.7 | |||
| 20.5 | 23.5 | 26.3 | 29.6 | 34.2 | 37.1 | 39.3 | |||
| 21.6 | 24.8 | 27.6 | 33.4 | 35.7 | 38.6 | 40.8 | |||
| 22.8 | 28.9 | 32.3 | 34.8 | 37.2 | 40.1 | 42.3 | |||
| 23.9 | 27.2 | 30.1 | 33.7 | 36.2 | 38.6 | 41.6 | 43.8 | ||
| 24.8 | 31.4 | 37.6 | 43.1 | 45.3 | |||||
| 27.3 | 30.8 | 33.9 | 37.7 | 40.3 | 42.7 | 45.9 | 48.3 | ||
| 29.6 | 33.2 | 36.4 | 40.3 | 45.5 | 48.7 | 51.2 | |||
| 31.8 | 35.6 | 38.9 | 42.9 | 45.6 | 48.2 | 51.5 | 54.1 | ||
| 37.9 | 41.3 | 45.4 | 48.3 | 54.3 | 56.9 | ||||
| 36.3 | 40.3 | 43.8 | 50.9 | 53.7 | 57.1 | 59.7 | |||
Распределение Стьюдента. Значения t=f(k,p)
Таблица П3.
| К | Р | ||||
| 0,9 | 0,95 | 0,98 | 0,99 | 0,999 | |
| 2,132 | 2,776 | 3,747 | 4,604 | 8,61 | |
| 2,015 | 2,571 | 3,365 | 4,032 | 6,859 | |
| 1,943 | 2,447 | 3,143 | 3,707 | 5,959 | |
| 1,859 | 2,365 | 2,998 | 3,499 | 5,405 | |
| 1,86 | 2,306 | 2,896 | 3,355 | 50,41 | |
| 1,833 | 2,262 | 2,821 | 3,25 | 4,781 | |
| 1,812 | 2,228 | 2,764 | 3,169 | 4,587 | |
| 1,796 | 2,201 | 2,718 | 3,106 | 4,487 | |
| 1,782 | 2,079 | 2,681 | 3,055 | 4,318 | |
| 1,771 | 2,06 | 2,65 | 3,012 | 4,221 | |
| 1,761 | 2,145 | 2,624 | 2,977 | 4,14 | |
| 1,753 | 2,131 | 2,602 | 2,497 | 4,073 | |
| 1,764 | 2,12 | 2,583 | 2,921 | 4,015 | |
| 1,734 | 2,103 | 2,552 | 2,878 | 3,922 | |
| 1,725 | 2,086 | 2,528 | 2,845 | 3,85 | |
| 1,708 | 2,06 | 2,485 | 2,787 | 3,725 | |
| 1,697 | 2,042 | 2,457 | 2,75 | 3,646 | |
| 1,689 | 2,03 | 2,437 | 2,724 | 3,591 | |
| 1,684 | 2,021 | 2,423 | 2,704 | 3,551 | |
| 1,679 | 2,014 | 2,412 | 2,689 | 3,522 | |
| 1,676 | 2,008 | 2,403 | 2,677 | 3,497 | |
| 1,671 | 2,39 | 2,66 | 3,46 | ||
| 1,667 | 1,995 | 2,381 | 2,648 | 3,436 | |
| 1,664 | 1,99 | 2,374 | 3,639 | 3,416 | |
| 1,662 | 1,987 | 2,368 | 2,632 | 3,401 | |
| 1,66 | 1,984 | 2,364 | 2,626 | 3,391 | |
| 1,645 | 1,96 | 2,326 | 2,576 | 3,291 |
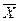 - оценка математического ожидания; n – объем выборки; Z
- оценка математического ожидания; n – объем выборки; Z 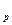 - такое значение аргумента функции Лапласа (табл.П2), при котором
- такое значение аргумента функции Лапласа (табл.П2), при котором
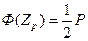 .
.
Функция Лапласа определяет площадь под кривой нормального распределения случайной величины Z с математическим ожиданием, равным 0, и дисперсией, равной 1, в промежутке от 0 до Z.
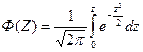 .
.
В табл. П2 приведены значения Ф(Z) для значений Z от 0 до 2,94; Ф(+∞)= 0,5.
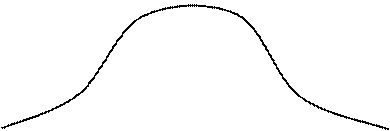
На рис. 3 показан принцип построения двустороннего доверительного интервала и нижнего одностороннего доверительного интервала.
 |
Ф(Z)


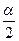 α
α 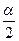
 |

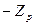
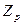
Рис. 3.
Как следует из рис.3, для уровня значимости α=1-р можно также записать, что:
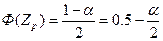 .
.
Верхний и нижний односторонние доверительные интервалы определяются, соответственно, выражениями,
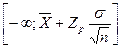 и
и 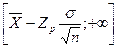 .
.
При этом Z 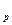 - такое значение аргумента функции Ф (Z) (табл. П2), при
- такое значение аргумента функции Ф (Z) (табл. П2), при
котором Ф(Z 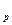 ) = 0,5 - α. Так как кривая нормального распределения
) = 0,5 - α. Так как кривая нормального распределения
симметрична, то при определении нижнего и двустороннего доверительного
интервалов используют ту же таблицу, что и для определения верхнего интервала.
Доверительный интервал для математического ожидания при
неизвестной дисперсии σ 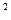 генеральной совокупности равен:
генеральной совокупности равен:
[ 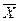 - t
- t 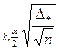 ], [
], [ 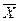 + t
+ t 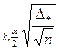 ],
],
где 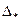 - несмещенная состоятельная оценка дисперсии (3); t
- несмещенная состоятельная оценка дисперсии (3); t 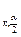 - аргумент функции плотности распределения Стьюдента, находится по табл. П3 для заданного уровня значимости и числа степеней свободы К, К=п-1.
- аргумент функции плотности распределения Стьюдента, находится по табл. П3 для заданного уровня значимости и числа степеней свободы К, К=п-1.
Кривая плотности распределения Стьюдента симметрична, поэтому односторонние доверительные интервалы находятся аналогично предыдущему случаю.
Для определения t 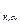 используется табл. ПЗ.
используется табл. ПЗ.
Принцип построения двустороннего и верхнего одностороннего доверительных интервалов поясняется на рис. 4, где t 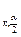 - критическая точка распределения
- критическая точка распределения
Стьюдента при двустороннем ограничении, t 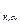 - при одностороннем.
- при одностороннем.

f(t)
-t 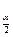 0 t
0 t 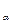 t
t 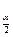
Рис.4.
Таблица П2.
| Z | Ф(Z) | Z | Ф(Z) | Z | Ф(Z) | Z | Ф(Z) |
| 1,6 | 0,4452 | 1,94 | 0,4738 | 2,28 | 0,4887 | 2,62 | 0,4956 |
| 1,62 | 0,4474 | 1,96 | 0,475 | 2,3 | 0,4883 | 2,64 | 0,4959 |
| 1,64 | 1,4495 | 1,98 | 0,4751 | 2,32 | 0,4898 | 2,66 | 0,4961 |
| 1,66 | 0,4515 | 0,4772 | 2,34 | 0,4904 | 2,68 | 0,4963 | |
| 1,68 | 0,4535 | 2,02 | 0,4783 | 2,36 | 0,4909 | 2,7 | 0,4965 |
| 1,7 | 0,4554 | 2,04 | 0,4793 | 2,38 | 0,4913 | 2,72 | 0,4967 |
| 1,72 | 0,4573 | 2,06 | 0,4803 | 2,4 | 0,4918 | 2,74 | 0,4969 |
| 1,74 | 0,4591 | 2,08 | 0,4812 | 2,42 | 0,4922 | 2,76 | 0,4971 |
| 1,76 | 0,4608 | 2,1 | 0,4821 | 2,44 | 0,4927 | 2,78 | 0,4973 |
| 1,78 | 0,4625 | 2,12 | 0,483 | 2,46 | 0,4931 | 2,8 | 0,4974 |
| 1,8 | 0,4648 | 2,14 | 0,4838 | 2,48 | 0,4934 | 2,82 | 0,4976 |
| 1,82 | 0,4656 | 2,16 | 0,4846 | 2,5 | 0,4938 | 2,84 | 0,4977 |
| 1,84 | ,04671 | 2,18 | 0,4854 | 2,52 | 0,4941 | 2,86 | 0,4979 |
| 1,86 | 0,4686 | 2,2 | 0,4861 | 2,54 | 0,4945 | 2,88 | 0,498 |
| 1,88 | 0,4699 | 2,22 | 0,4868 | 2,56 | 0,4948 | 2,9 | 0,4981 |
| 1,9 | 0,4713 | 2,24 | 0,4875 | 2,58 | 0,4951 | 2,92 | 0,4982 |
| 1,92 | 0,4726 | 2,26 | 0,4881 | 2,6 | 0,4953 | 2,94 | 0,4984 |
Таблица П1.
| Объем выборки | Уровень значимости | |||||
| 0,05 | 0,01 | |||||
 | 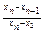 | 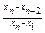 | 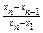 | 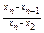 | 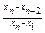 | |
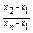 | 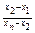 | 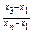 | 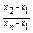 | 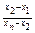 | 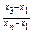 | |
| 0,941 | 0,998 | |||||
| 0,765 | 0,955 | 0,967 | 0,889 | 0,991 | 0,992 | |
| 0,642 | 0,807 | 0,845 | 0,78 | 0,916 | 0,929 | |
| 0,56 | 0,689 | 0,736 | 0,698 | 0,805 | 0,836 | |
| 0,507 | 0,61 | 0,661 | 0,637 | 0,74 | 0,778 | |
| 0,468 | 0,554 | 0,607 | 0,59 | 0,683 | 0,71 | |
| 0,437 | 0,512 | 0,565 | 0,555 | 0,635 | 0,667 | |
| 0,412 | 0,477 | 0,531 | 0,527 | 0,597 | 0,632 | |
| 0,392 | 0,45 | 0,504 | 0,502 | 0,566 | 0,603 | |
| 0,376 | 0,428 | 0,481 | 0,482 | 0,541 | 0,579 | |
| 0,338 | 0,381 | 0,43 | 0,438 | 0,486 | 0,522 | |
| 0,3 | 0,334 | 0,372 | 0,391 | 0,43 | 0,464 | |
| 0,281 | 0,309 | 0,347 | 0,367 | 0,4 | 0,434 | |
| 0,26 | 0,283 | 0,322 | 0,341 | 0,369 | 0,402 |
Доверительные интервалы для дисперсии определяются с помощью
распределения  Пирсона, как для случая известного, так и неизвестного значений математического ожидания случайной величины X, расчетные формулы различаются здесь лишь числом степеней свободы и видом оценки дисперсии σ
Пирсона, как для случая известного, так и неизвестного значений математического ожидания случайной величины X, расчетные формулы различаются здесь лишь числом степеней свободы и видом оценки дисперсии σ 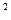 .
.
Доверительный интервал для дисперсии при известном математическое ожидании μ случайной величины X определяется выражением
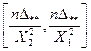 , (9)
, (9)
где п - объем выборки; 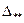 - состоятельная несмещенная и эффективная оценка дисперсии;
- состоятельная несмещенная и эффективная оценка дисперсии; 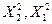 - аргументы функции плотности распределения Пирсона (табл. П4); площадь под кривой плотности, заключенная между точками
- аргументы функции плотности распределения Пирсона (табл. П4); площадь под кривой плотности, заключенная между точками 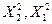 равна выбранному значению доверительной вероятности Р.
равна выбранному значению доверительной вероятности Р.
Кривая плотности распределения Пирсона показана на рис. 5 для числа степенен свободы К=1,2 и 6. При построении двустороннего доверительного интервала точки 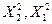 , выбираются так, чтобы Р{
, выбираются так, чтобы Р{  <
< 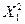 }=Р{
}=Р{  >
> 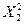 }=
}= 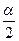 , т.е. так, чтобы заштрихованные площадки на рис. 6 были одинаковы и равны
, т.е. так, чтобы заштрихованные площадки на рис. 6 были одинаковы и равны 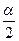 .
.
Значения 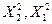 находятся по таблице для выбранной доверительной вероятности Р и числа степеней свободы К= п. Односторонний доверительный интервал определяется выражением:
находятся по таблице для выбранной доверительной вероятности Р и числа степеней свободы К= п. Односторонний доверительный интервал определяется выражением:
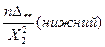 и
и 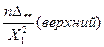 ,
,
где Р{  >
> 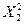 }= α и Р {
}= α и Р {  >
> 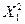 }=1- α.
}=1- α.
Принцип построения двустороннего и одностороннего доверительных интервалов показан на рис.6.











 f(
f( )
)
k=1
k=2
k=6
Рис.5  Рис.6.
Рис.6.
Доверительный интервал для дисперсии при неизвестном математическом ожидании случайной величины X определяется выражением:
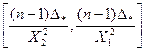 , (10)
, (10)
где n - объем выборки; 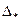 - состоятельная и несмещенная оценка дисперсии;
- состоятельная и несмещенная оценка дисперсии; 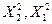 - критические точки распределения Пирсона, находятся по таблице П4 для числа степеней свободы k=n-l.
- критические точки распределения Пирсона, находятся по таблице П4 для числа степеней свободы k=n-l.
В большинстве практических случаев определяют верхний односторонний доверительный интервал для дисперсии, тем самым фиксируя верхнюю границу степени разброса исследуемого параметра с уровнем значимости α.
 2015-10-13
2015-10-13 2309
2309
