а)Вероятности,связанные с нормальным распределением, можно вычислять, используя функцию НОРМРАСП. Данная функция, при значении параметра интегральная равном ИСТИНА(1), возвращает значения функции распределения 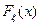 нормальной случайной величины. Поскольку
нормальной случайной величины. Поскольку 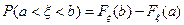 , то
, то
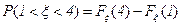 =
=
=НОРМРАСП(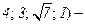 НОРМРАСП(
НОРМРАСП(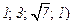 =0,422426.
=0,422426.
б) Квантили, критические точки и, вообще, различные значения, связанные с вероятностями для нормальной случайной величины, можно вычислять, используя функцию НОРМОБР или НОРМСТОБР. Функция НОРМОБР возвращает квантиль нормального распределения для указанной вероятности, то есть НОРМОБР(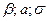 ) =
) = 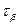 , для которого
, для которого 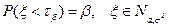 . Таким образом, квантиль уровня 0,85 равна
. Таким образом, квантиль уровня 0,85 равна 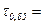 НОРМОБР(
НОРМОБР(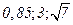 )=5,742.
)=5,742.
в) Критическая точка уровня 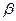 по определению есть значение
по определению есть значение 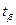 , для которого
, для которого 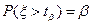 . Критическая точка уровня
. Критическая точка уровня 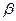 совпадает с квантилью уровня
совпадает с квантилью уровня 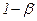 . Поэтому, критическая точка уровня 0,07 есть
. Поэтому, критическая точка уровня 0,07 есть 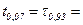 НОРМОБР(
НОРМОБР(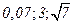 )=6,905.
)=6,905.
г) Требуется найти такое значение 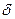 , для которого
, для которого 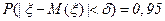 . Удобнее в данном случае воспользоваться функцией НОРМСТОБР, которая возвращает квантиль стандартного нормального распределения для указанной вероятности. Имеем:
. Удобнее в данном случае воспользоваться функцией НОРМСТОБР, которая возвращает квантиль стандартного нормального распределения для указанной вероятности. Имеем: 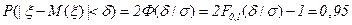 , где
, где 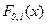 - функция распределения стандартной нормальной величины. Или
- функция распределения стандартной нормальной величины. Или 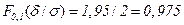 . Используя НОРМСТОБР, находим квантиль для стандартной нормальной величины уровня 0,975:
. Используя НОРМСТОБР, находим квантиль для стандартной нормальной величины уровня 0,975: 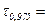 НОРМСТОБР(
НОРМСТОБР(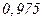 )=1,96. Тогда
)=1,96. Тогда 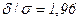 , откуда
, откуда 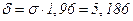 . Таким образом, искомый интервал имеет вид:
. Таким образом, искомый интервал имеет вид: 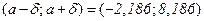 .
.
 2015-10-13
2015-10-13 570
570








