Статистические функции пакета EXEL
· БИНОМРАСП (число успехов; число испытаний; вероятность успеха; интегральная)
Возвращает вероятности связанные с биномиальным распределением. Функция БИНОМРАСП используется для подсчета вероятностей числа успехов в испытаниях по схеме Бернулли.
Число успехов — количество успешных испытаний (m).
Число испытаний — общее число независимых испытаний (n).
Вероятность успеха — вероятность успеха в каждом испытании (p).
Интегральная — это логическое значение, определяющее форму функции. Если аргумент интегральная имеет значение ИСТИНА (1), то функция БИНОМРАСП возвращает вероятность того, что число успешных испытаний не более значения число успехов; если этот аргумент имеет значение ЛОЖЬ (0), то возвращается вероятность того, что число успешных испытаний в точности равно значению аргумента число успехов.
Таким образом:
БИНОМРАСП (m; n; p; 0) = 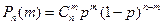 ;
;
БИНОМРАСП (m; n; p; 1) = 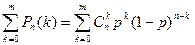 .
.
· ПУАССОН (x; среднее; интегральная)
Возвращает вероятности, связанные с распределением Пуассона (например, вероятности числа событий в простейшем потоке за некоторый промежуток времени, при известном среднем числе событий)
x — количество событий.
Среднее — среднее число событий (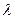 ).
).
Интегральная — логическое значение, определяющее форму возвращаемого распределения вероятностей. Если аргумент «интегральная» имеет значение ИСТИНА (1), то функция ПУАССОН возвращает вероятность того, что число случайных событий будет от 0 до x включительно. Если этот аргумент имеет значение ЛОЖЬ (0), то возвращается вероятность того, что событий будет в точности x.
Таким образом: ПУАССОН (x; λ; 0) = 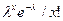 :ПУАССОН (x; λ; 1) =
:ПУАССОН (x; λ; 1) = 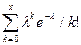 .
.
· ГИПЕРГЕОМЕТ (число успехов в выборке; размер выборки; число успехов в совокупности; размер совокупности)
Возвращает вероятности для гипергеометрического распределения. ГИПЕРГЕОМЕТ возвращает вероятность заданного количества успехов в выборке, если заданы размер выборки, количество успехов в генеральной совокупности и размер генеральной совокупности.
Число успехов в выборке — это количество успешных испытаний в выборке (m).
Размер выборки — размер выборки (n).
Число успехов в совокупности — количество успешных испытаний в генеральной совокупности (M).
Размер совокупности — размер генеральной совокупности (N).
Например, из генеральной совокупности, содержащей N шаров, среди которых M красных, выбирается наудачу n шаров. Тогда, вероятность того, что среди них ровно m красных равна: 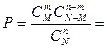 ГИПЕРГЕОМЕТ(m; n; M; N).
ГИПЕРГЕОМЕТ(m; n; M; N).
· НОРМРАСП (x; среднее; стандартное откл; интегральная)
Возвращает вероятности, связанные с нормальным распределением.
x — значение, для которого определяется вероятность.
Среднее — математическое ожидание распределения (a).
Стандартное откл — среднеквадратическое отклонение распределения (σ).
Интегральная — логическое значение, определяющее форму функции. Если интегральная имеет значение ИСТИНА (1), то функция НОРМРАСП возвращает функцию распределения от аргумента 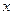 ; если это аргумент имеет значение ЛОЖЬ (1), то возвращается плотности распределения от аргумента
; если это аргумент имеет значение ЛОЖЬ (1), то возвращается плотности распределения от аргумента 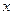 .
.
Таким образом:
НОРМРАСП(x; a; σ; 0) 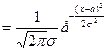 ;
;
НОРМРАСП(x; a; σ; 1) 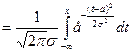 .
.
· НОРМСТРАСП (z)
Возвращает функцию распределения стандартной нормальной величины, т.е. НОРМСТРАСП(z) = 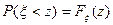 , где
, где 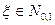 ,
, 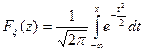 .
.
· НОРМОБР (вероятность; среднее; стандартное откл)
Возвращает квантиль нормального распределения для указанной вероятности, то есть НОРМСТОБР(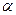 ) возвращает значение
) возвращает значение 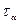 , для которого
, для которого 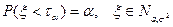 .
.
Вероятность — вероятность, соответствующая квантили.
Среднее — математическое ожидание распределения.
Стандартное откл — среднеквадратическое отклонение распределения.
· НОРМСТОБР (вероятность)
Возвращает квантиль стандартного нормального распределения для указанной вероятности, то есть НОРМСТОБР(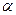 ) возвращает значение
) возвращает значение 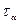 , для которого
, для которого 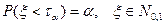
Вероятность — вероятность, соответствующая квантили.
· СТЬЮДРАСП (x; степени свободы; хвосты)
Возвращает вероятности, связанные с распределением Стьюдента.
x — численное значение, для которого требуется вычислить вероятности.
Степени свободы — число степеней свободы распределения.
Хвосты — число учитываемых хвостов распределения. Если хвосты = 1, то функция СТЬЮДРАСП возвращает вероятность того, что случайная величина, распределенная по закону Стьюдента, примет значение большее чем 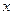 . Т.е. СТЬЮДРАСП(x; n; 1) =
. Т.е. СТЬЮДРАСП(x; n; 1) = 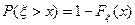 , где
, где 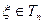 . Если хвосты = 2, то функция СТЬЮДРАСП возвращает вероятность того, что случайная величина, распределенная по закону Стьюдента, примет значение, большее, чем
. Если хвосты = 2, то функция СТЬЮДРАСП возвращает вероятность того, что случайная величина, распределенная по закону Стьюдента, примет значение, большее, чем 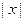 . Т.е. СТЬЮДРАСП(x; n; 2) =
. Т.е. СТЬЮДРАСП(x; n; 2) = 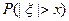 , где
, где 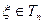 .
.
· СТЬЮДРАСПОБР (вероятность; степени свободы)
возвращает коэффициент Стьюдента 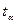 (двухстороннюю критическую точку уровня
(двухстороннюю критическую точку уровня 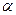 ), соответствующий заданной вероятности
), соответствующий заданной вероятности 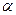 : т.е. значение
: т.е. значение 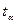 для которого
для которого 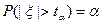 , что тоже самое, что квантиль распределения Стьюдента уровня
, что тоже самое, что квантиль распределения Стьюдента уровня 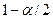 , то есть значение
, то есть значение 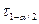 , для которого
, для которого 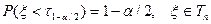 .
.
Вероятность — вероятность, для которой находится значение коэффициента.
Степени свободы — число степеней свободы, характеризующее распределение.
· ХИ2РАСП (x; степени свободы)
Возвращает вероятность того, что случайная величина, распределенная по закону хи-квадрат примет значение, большее, чем 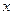 , т.е. ХИ2РАСП(x; n ) =
, т.е. ХИ2РАСП(x; n ) = 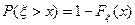 , где
, где 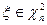 .
.
x — это значение, для которого требуется вычислить вероятность.
Степени свободы — это число степеней свободы распределения хи-квадрат.
· ХИ2ОБР (вероятность; степени свободы)
возвращает критическую точку распределения хи-квадрат для заданной вероятности, то есть ХИ2ОБР(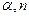 )=
)= 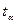 , где
, где 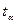 значение, для которого
значение, для которого 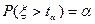 , что тоже самое, что квантиль распределения хи-квадрат уровня
, что тоже самое, что квантиль распределения хи-квадрат уровня 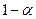 .
.
Вероятность — вероятность, для которой находится критическая точка.
Степени свободы — число степеней свободы, характеризующее распределение.
· FРАСП (x; степени свободы1; степени свободы2)
Возвращает вероятность того, что случайная величина, распределенная по закону Фишера примет значение, большее, чем 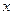 , т.е. FРАСП(x; n1; n2) =
, т.е. FРАСП(x; n1; n2) = 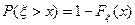 , где
, где 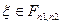 .
.
x — это значение, для которого требуется вычислить вероятность.
Степени свободы1, степени свободы2 — число степеней свободы, характеризующих распределение.
· FРАСПОБР (вероятность; степени свободы1; степени свободы2)
возвращает критическую точку распределения Фишера для заданной вероятности, то есть FРАСПОБР(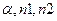 )=
)= 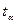 , где
, где 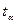 значение, для которого
значение, для которого 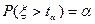 , что тоже самое, что квантиль распределения Фишера уровня
, что тоже самое, что квантиль распределения Фишера уровня 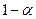 .
.
Вероятность — вероятность, для которой находится критическая точка.
Степени свободы1, степени свободы2 — число степеней свободы, характеризующих распределение.
 2015-10-13
2015-10-13 1343
1343