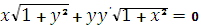
Преобразуем исходное уравнение
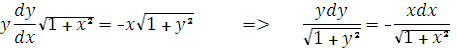
Интегрируя, имеем
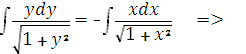
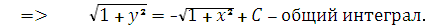
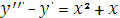
Общее решение ищем в виде
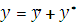
Соответствующее однородное уравнение имеет вид
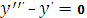
Поскольку корни характеристического уравнения 
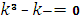
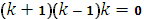
действительны и различны 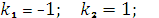
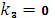 , то общее решение однородного уравнения имеет вид
, то общее решение однородного уравнения имеет вид
Правая часть исходного уравнения имеет вид
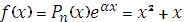
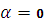 является одним корнем характеристического уравнения, поэтому частное решение
является одним корнем характеристического уравнения, поэтому частное решение 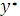 ищем в виде
ищем в виде
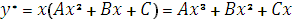
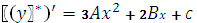
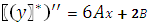
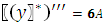
Подставляя 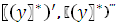 в исходное уравнение получим
в исходное уравнение получим
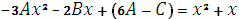
Приравнивая коэффициенты при одинаковых степенях x, получим
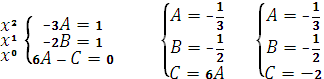
Тогда
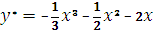
Общее решение имеет вид
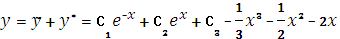
Задание №57. Найти частное решение однородного дифференциального уравнения.
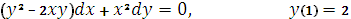
 2015-10-13
2015-10-13 185
185








