Решение

Преобразуем заданное уравнение:

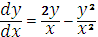
Поскольку

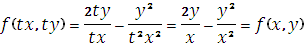
то исходное уравнение является однородным и применяется замена:

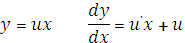
Тогда

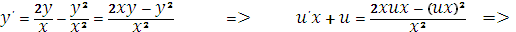
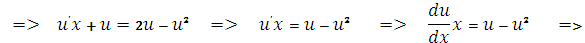
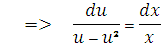
Интегрируя, имеем

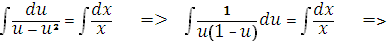
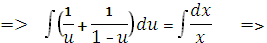
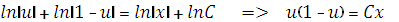
Заменяя 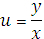получим общий интеграл исходного уравнения

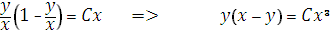
Из начального условия 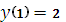имеем

Тогда 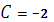и частный интеграл дифференциального уравнения, удовлетворяющее начальному условию, имеет вид

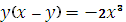
Задание №62. В партии из 22 изделий половина бракованных. Наудачу выбираются 5 изделий. Найти вероятность того, что выбранные изделия доброкачественные.