Сжатие графика функции к оси ординат

Это случай когда АРГУМЕНТ функции умножен на число, бОльшее единицы.

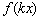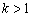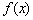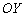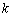Правило: чтобы построить график функции , где , нужно график функции сжать к оси в раз.

И первым на эшафот взойдёт функция, которой я недавно грозился:

Пример 1

Построить график функции .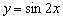

Сначала изобразим график синуса, его период равен :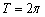

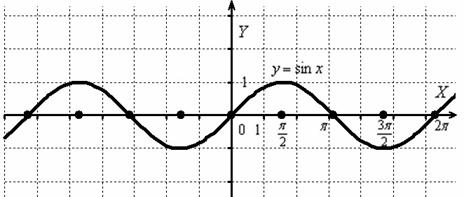
К слову, чертить графики тригонометрических функций вручную – занятие кропотливое, поскольку 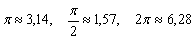и т.д., то есть на стандартной клетчатой бумаге аккуратным нужно быть вплоть до миллиметра, даже до полумиллиметра. Впрочем, многие с этим уже столкнулись.

Теперь поиграем на бесконечно длинном баяне. Мысленно возьмём синусоиду в руки и сожмём её к оси в 2 раза:

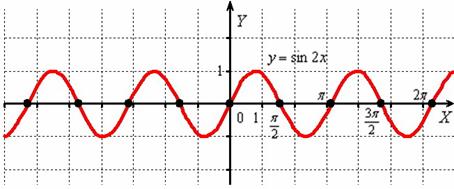
То есть, график функции 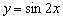получается путём сжатия графика 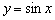к оси ординат в два раза. Логично, что период итоговой функции тоже уполовинился: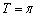

В целях самоконтроля можно взять 2-3 значения «икс» и устно либо на черновике выполнить подстановку:

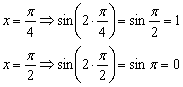
Смотрим на чертёж, и видим, что это действительно так.

Аналогичную блиц-проверку полезно осуществлять в любом другом примере! Более того, она лучше поможет усвоить суть того или иного преобразования.

Пример 2

Построить график функции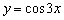

«Чёрная гармошка» 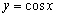сжимается к оси 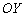в 3 раза:

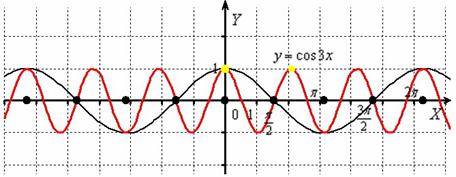
Итоговый график 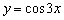проведён красным цветом.
Исходный период 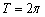косинуса закономерно уменьшается в три раза: 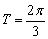(отграничен жёлтыми точками).