Определение. Достаточные признаки монотонности функции

Достаточные признаки монотонности функции.

Исследование функции

Если функция f (x) дифференцируема в некоторой точке, то она непрерывна в этой точке.
Обратное неверно: непрерывная функция может не иметь производной.

Например, функция y = | x | всюду непрерывна, но она не имеет производной при x = 0, так как в этой точке не существует касательной к графику этой функции.

Следствие. Если функция разрывна в некоторой точке, то она не имеет производной в этой точке.

• Если f '(x) > 0 в каждой точке интервала (a, b), то функция f (x) возрастает на этом интервале.
• Если f '(x) < 0 в каждой точке интервала (a, b), то функция f (x) убывает на этом интервале.

Теорема Дарбу. Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак.

Используя эти интервалы, можно найти интервалы монотонности функций, что очень важно при их исследовании.

Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками этой функции.

Эти точки очень важны при анализе функции и построении её графика, потому что только в этих точках функция может иметь экстремум (минимум или максимум).

Необходимое условие экстремума. Если x₀ - точка экстремума функции f ( x) и производная f’ существует в этой точке, то f ’ (x₀) = 0.

Эта теорема - необходимое условие экстремума. Если производная функции в некоторой точке равна 0, то это не значит, что функция имеет экстремум в этой точке.

Например, производная функции f (x) = x ³ равна 0 при x = 0, но эта функция не имеет экстремум в этой точке.
С другой стороны, функция y = | x |, имеет минимум в точке x = 0, но в этой точке производной не существует.

Достаточные условия экстремума.

• Если производная при переходе через точку x₀ меняет свой знак с плюса на минус, то x₀ - точка максимума.
• Если производная при переходе через точку x₀ меняет свой знак с минуса на плюс, то x₀ - точка минимума.

Общая схема исследования функции и построение ее графика:

• найти область определения и область значений функции,
• установить, является ли функция чётной или нечётной,
• определить, является ли функция периодической или нет,
• найти нули функции и её значения при x = 0,
• найти интервалы знакопостоянства,
• найти интервалы монотонности,
• найти точки экстремума и значения функции в этих точках,
• проанализировать поведение функции вблизи “особых” точек

Уравнение вида

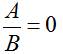
где А, В - многочлены, называется рациональным.

Например, 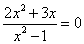. Подобное уравнение 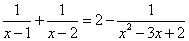возможно привести к рациональному, преобразовав его.