Линейная функция
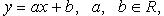
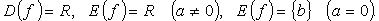
Функция строго возрастает при a > 0, строго убывает при a < 0. График функции - прямая линия.
Квадратичная функция
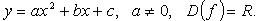
1. При a > 0
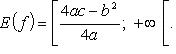
Функция строго убывает на 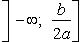 и строго возрастает на
и строго возрастает на 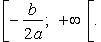 График функции - парабола с осью x = - b/(2a), вершиной в точке
График функции - парабола с осью x = - b/(2a), вершиной в точке 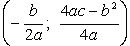 и ветвями, направленными вверх.
и ветвями, направленными вверх.
2. При a > 0
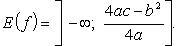
Функция строго убывает на 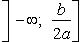 и строго возрастает на
и строго возрастает на 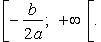 График функции - парабола с осью x = - b/(2a), вершиной в точке
График функции - парабола с осью x = - b/(2a), вершиной в точке 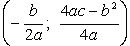 и ветвями, направленными вверх.
и ветвями, направленными вверх.
Степенная функция 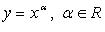
1. 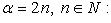
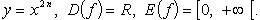
Функция четная, строго убывает на 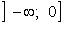 и строго возрастает на
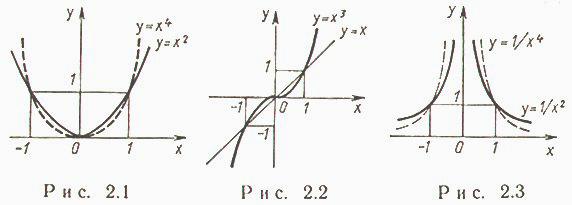
и строго возрастает на 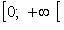 (рис. 2.1).
(рис. 2.1).
2. 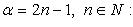
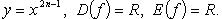
Функция нечетная, строго возрастает (рис. 2.2).
3. 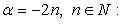
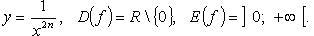
Функция четная, строго возрастает на 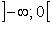 и строго убывает на
и строго убывает на 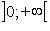 (рис. 2.3).
(рис. 2.3).
4. 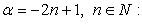
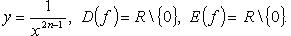
Функция нечетная, строго убывает на 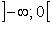 и
и 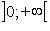 (рис. 2.4).
(рис. 2.4).
5. 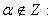
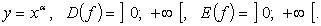
При некоторых 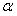 D(f) и E(f) могут быть шире.
D(f) и E(f) могут быть шире.
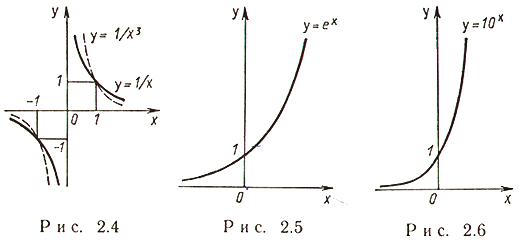
Экспонента (рис. 2.5)
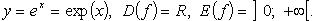
Функция строго возрастает.
Показательная функция (рис. 2.6)
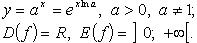
При 0 < a < 1 функция строго убывает, при a > 1 строго возрастает.
Логарифмическая функция
Логарифм натуральный (рис. 2.7)
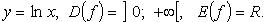
Функция строго возрастает.
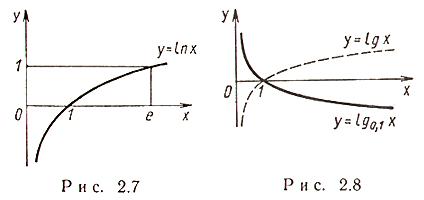
Логарифм с основанием a (рис. 2.8)
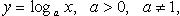
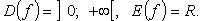
При 0 < a < 1 ф. строго убывает, при a > 1 строго возрастает.
Тригонометрические функции
1. 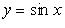 (рис. 2.9):
(рис. 2.9):
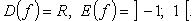
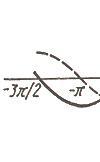
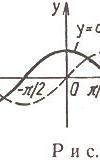
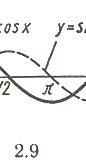
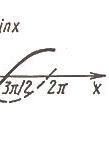
Функция нечетная. Период 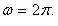 На каждом из промежутков
На каждом из промежутков 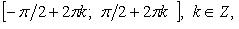 ф. строго возрастает, на
ф. строго возрастает, на 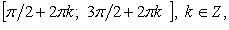 строго убывает.
строго убывает.
2. 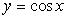 (рис. 2.9):
(рис. 2.9):
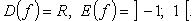
Функция четная. Период 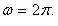 На каждом из промежутков
На каждом из промежутков 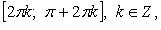 ф. строго убывает, на
ф. строго убывает, на 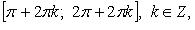 строго возрастает.
строго возрастает.
3. 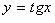 (рис. 2.10):
(рис. 2.10):
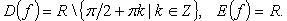
Функция нечетная. Период 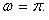 Функция строго возрастает на каждом из промежутков
Функция строго возрастает на каждом из промежутков 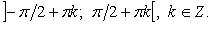
4. 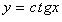 (рис. 2.11):
(рис. 2.11):
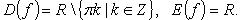
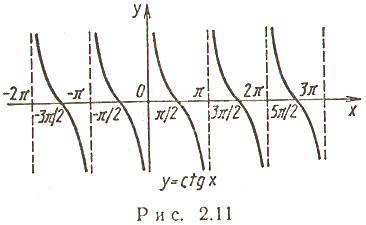
Функция нечетная. Период 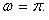 Функция строго убывает на каждом из промежутков
Функция строго убывает на каждом из промежутков 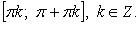
Обратные тригонометрические функции
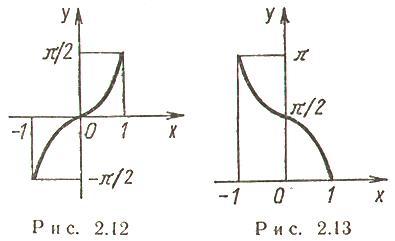
1. 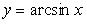 (рис. 2.12):
(рис. 2.12):
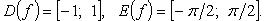
Функция нечетная, строго возрастает.
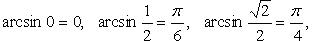
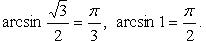
2. 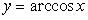 (рис. 2.13):
(рис. 2.13):
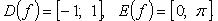
Функция строго убывает
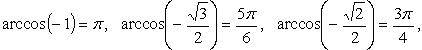
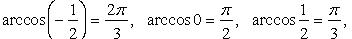
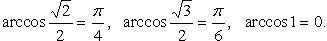
3. 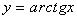 (рис. 2.14):
(рис. 2.14):
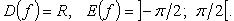
Функция нечетная, строго возрастает.
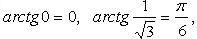
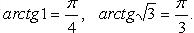
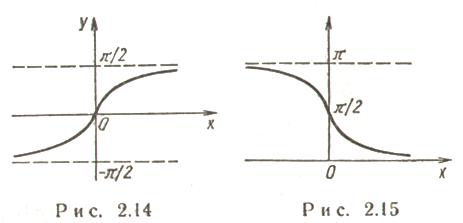
4. 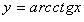 (рис. 2.15):
(рис. 2.15):
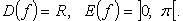
Функция строго убывает
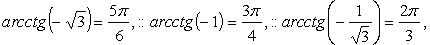
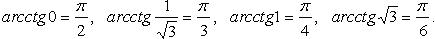
Вычисление значений тригонометрических функций от обратных тригонометрических
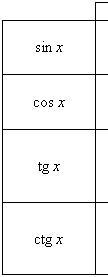
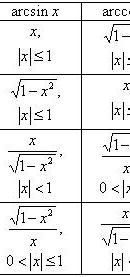
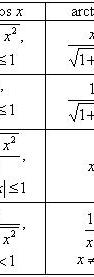
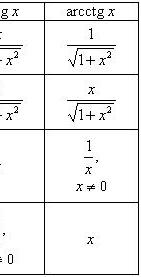
Преобразование сумм обратных тригонометрических функций
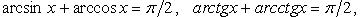
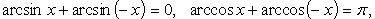
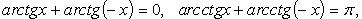
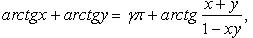
где
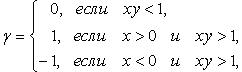
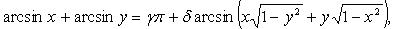
где 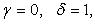 если
если 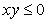 или
или 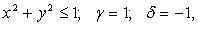 если x >0, y > 0 и
если x >0, y > 0 и 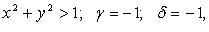 если x < 0, y < 0 и
если x < 0, y < 0 и 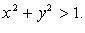
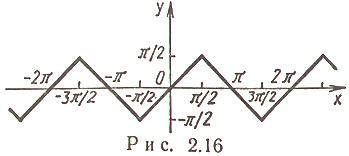
Обратные тригонометрические функции от тригонометрических функций
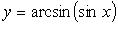 (рис. 2.16).
(рис. 2.16).
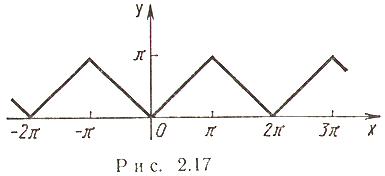
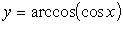 (рис. 2.17).
(рис. 2.17).
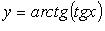 (рис. 2.18).
(рис. 2.18).
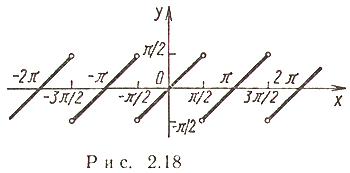
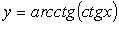 (рис. 2.19).
(рис. 2.19).
Гиперболические функции
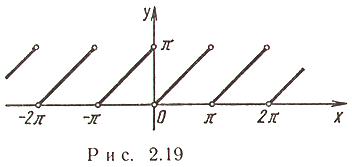
1. Синус гиперболический (рис. 2.20) 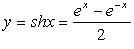 :
:
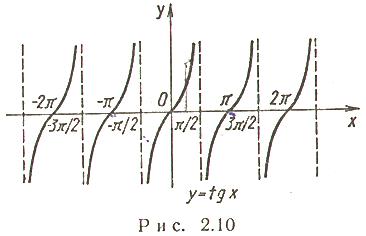
D(f) = R, E(f) = R.
Функция нечетная, строго возрастает.
2. Косинус гиперболический (рис. 2.20) 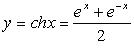 :
:
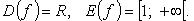
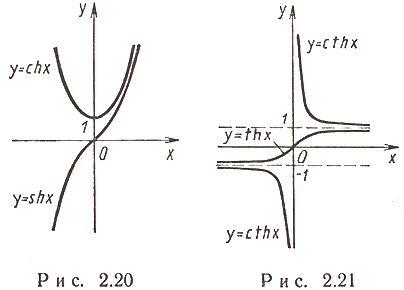
Функция четная, строго убывает на 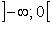 и строго возрастает на
и строго возрастает на 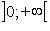
3. Тангенс гиперболический (рис. 2.21) 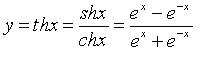 :
:
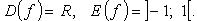
Функция нечетная, строго возрастает.
4. Котангенс гиперболический (рис. 2.21) 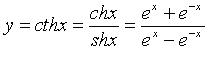 :
:
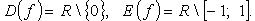
Функция нечетная, убывает на промежутках 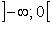 и
и 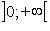
Обратные гиперболические функции
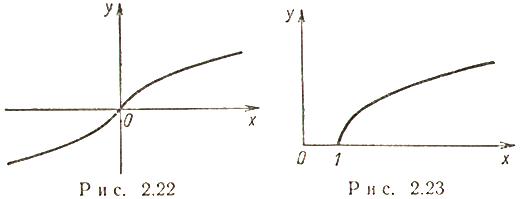
1. Ареасинус (рис. 2.22) 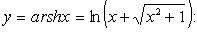
D(f) = R, E(f) = R.
Функция нечетная, строго возрастает.
2. Ареакосинус (рис. 2.23) 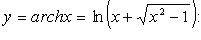
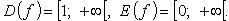
Функция строго возрастает.
3. Ареатангенс (рис. 2.24) 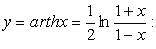
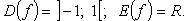
Функция нечетная, строго возрастает.
4. Ареакотангенс (рис. 2.25) 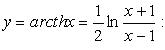
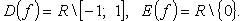
Функция нечетная, строго убывает на 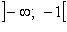 и
и 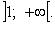
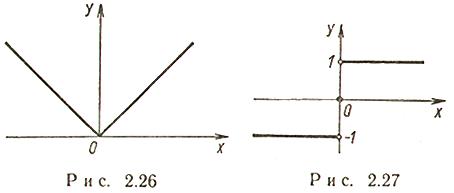
Функция модуль (рис. 2.26)
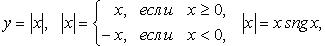
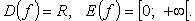
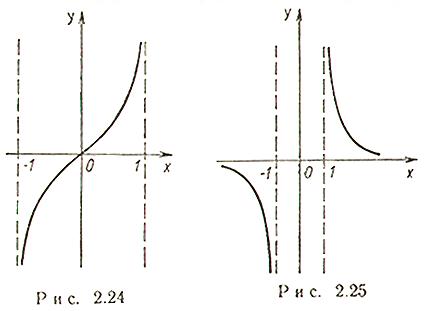
Функция четная, строго убывает на 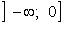 и строго возрастает на
и строго возрастает на 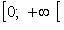
Некоторые кусочно-постоянные функции
1. Функция сигнум (рис. 2.27)
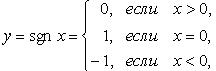
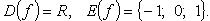
Функция нечетная, возрастающая.
2. Функция единичного скачка (функция Хевисайда)(рис. 2.28)
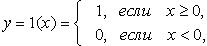
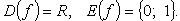
Функция возрастающая.
3. Селектор точки x = 0: s(x) = 1(x)*1(1-x).
4. Селектор отрезка [0; 1]: s(x; 0; 1) = 1(x)*1(1-x).
5. Функция антье (целая часть) (рис. 2. 29): y = [x]. Если x = n + r, где 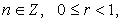 то [x] = n; [x] - наибольшее целое число, не превосходящее x; D(f) = R, E(f) = Z. Функция возрастающая.
то [x] = n; [x] - наибольшее целое число, не превосходящее x; D(f) = R, E(f) = Z. Функция возрастающая.
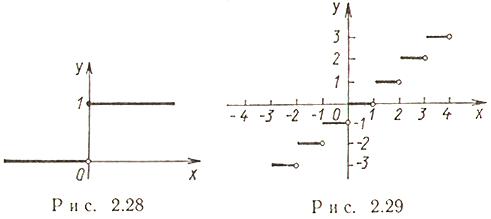
Функция Дирихле
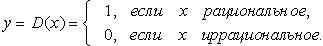
 2014-02-24
2014-02-24 1271
1271
