Если к АРГУМЕНТУ функции добавляется константа, то происходит сдвиг (параллельный перенос) графика вдоль оси 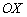 . Рассмотрим функцию
. Рассмотрим функцию 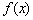 и положительное число
и положительное число 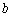 :
:
Правила:
1) чтобы построить график функции 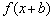 , нужно график
, нужно график 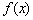 сдвинуть ВДОЛЬ оси
сдвинуть ВДОЛЬ оси 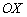 на
на 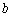 единиц влево;
единиц влево;
2) чтобы построить график функции 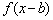 , нужно график
, нужно график 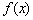 сдвинуть ВДОЛЬ оси
сдвинуть ВДОЛЬ оси 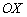 на
на 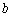 единиц вправо.
единиц вправо.
Пример 6
Построить график функции 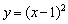
Берём параболу 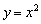 и сдвигаем её вдоль оси абсцисс на 1 единицу вправо:
и сдвигаем её вдоль оси абсцисс на 1 единицу вправо:
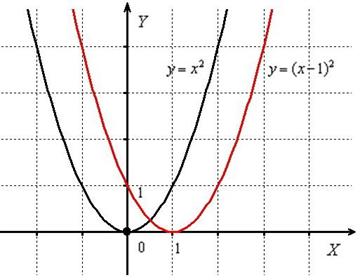
«Опознавательным маячком» служит значение 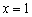 , именно здесь находится вершина параболы
, именно здесь находится вершина параболы 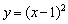 .
.
Теперь, думаю, ни у кого не возникнет трудностей с построением графика 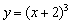 (демонстрационный пример начала урока) – кубическую параболу
(демонстрационный пример начала урока) – кубическую параболу 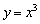 нужно сдвинуть на 2 единицы влево.
нужно сдвинуть на 2 единицы влево.
Вот ещё один характерный случай:
Пример 7
Построить график функции 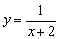
Гиперболу 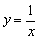 (чёрный цвет) сдвинем вдоль оси
(чёрный цвет) сдвинем вдоль оси  на 2 единицы влево:
на 2 единицы влево:
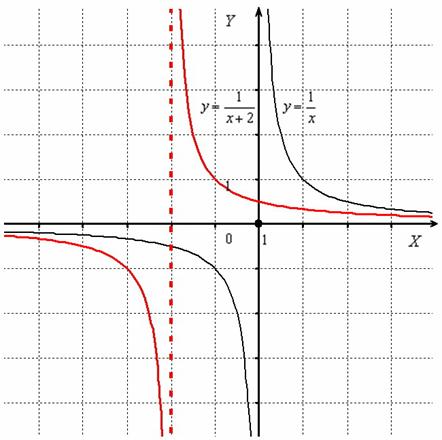
Перемещение гиперболы «выдаёт» значение, которое не входит в область определения функции. В данном примере 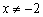 , и уравнение прямой
, и уравнение прямой 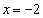 задаёт вертикальную асимптоту (красный пунктир) графика функции
задаёт вертикальную асимптоту (красный пунктир) графика функции 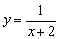 (красная сплошная линия). Таким образом, при параллельном переносе асимптота графика тоже сдвигается (что очевидно).
(красная сплошная линия). Таким образом, при параллельном переносе асимптота графика тоже сдвигается (что очевидно).
Вернёмся к тригонометрическим функциям:
Пример 8
Построить график функции 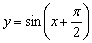
График синуса 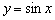 (чёрный цвет) сдвинем вдоль оси вдоль оси
(чёрный цвет) сдвинем вдоль оси вдоль оси 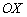 на
на 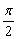 влево:
влево:
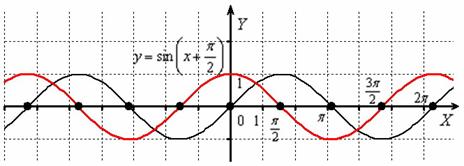
Внимательно присмотримся к полученному красному графику 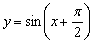 …. Это в точности график косинуса
…. Это в точности график косинуса 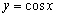 ! По сути, мы получили геометрическую иллюстрацию формулы приведения
! По сути, мы получили геометрическую иллюстрацию формулы приведения 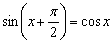 , и перед вами, пожалуй, самая «знаменитая» формула, связывающая данные тригонометрические функции. График функции
, и перед вами, пожалуй, самая «знаменитая» формула, связывающая данные тригонометрические функции. График функции 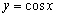 получается путём сдвига синусоиды
получается путём сдвига синусоиды 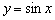 вдоль оси
вдоль оси 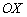 на
на 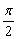 единиц влево (о чём уже говорилось на уроке Графики и свойства элементарных функций). Аналогично можно убедиться в справедливости любой другой формулы приведения.
единиц влево (о чём уже говорилось на уроке Графики и свойства элементарных функций). Аналогично можно убедиться в справедливости любой другой формулы приведения.
Рассмотрим композиционное правило, когда аргумент представляет собой линейную функцию: 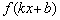 , при этом параметр «ка» не равен нулю или единице, параметр «бэ» – не равен нулю. Как построить график такой функции? Из школьного курса мы знаем, что, что умножение имеет приоритет перед сложением, поэтому, казалось бы, сначала график сжимаем/растягиваем/отображаем в зависимости от значения
, при этом параметр «ка» не равен нулю или единице, параметр «бэ» – не равен нулю. Как построить график такой функции? Из школьного курса мы знаем, что, что умножение имеет приоритет перед сложением, поэтому, казалось бы, сначала график сжимаем/растягиваем/отображаем в зависимости от значения 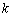 , а потом сдвигаем на
, а потом сдвигаем на 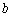 единиц. Но здесь есть подводный камень, и корректный алгоритм таков:
единиц. Но здесь есть подводный камень, и корректный алгоритм таков:
Аргумент функции необходимо представить в виде 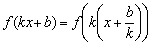 и последовательно выполнить следующие преобразования:
и последовательно выполнить следующие преобразования:
1) График функции 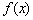 сжимаем (или растягиваем) к оси (от оси) ординат:
сжимаем (или растягиваем) к оси (от оси) ординат: 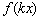 (если
(если 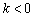 , то график дополнительно следует отобразить симметрично относительно оси
, то график дополнительно следует отобразить симметрично относительно оси 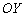 ).
).
2) График полученной функции 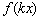 сдвигаем влево (или вправо) вдоль оси абсцисс на
сдвигаем влево (или вправо) вдоль оси абсцисс на 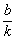 (!!!) единиц, в результате чего будет построен искомый график
(!!!) единиц, в результате чего будет построен искомый график 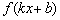 .
.
Пример 9
Построить график функции 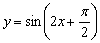
Представим функцию в виде 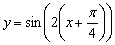 и выполним следующие преобразования: синусоиду
и выполним следующие преобразования: синусоиду 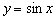 (чёрный цвет):
(чёрный цвет):
1) сожмём к оси 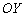 в два раза:
в два раза: 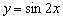 (синий цвет);
(синий цвет);
2) сдвинем вдоль оси 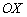 на
на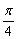 (!!!) влево:
(!!!) влево: 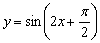 (красный цвет):
(красный цвет):
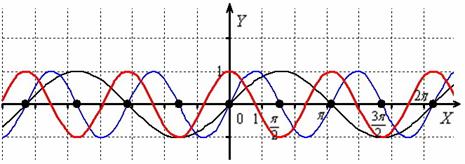
Пример вроде бы несложный, а пролететь с параллельным переносом легче лёгкого. График сдвигается на 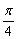 , а вовсе не на
, а вовсе не на 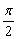 .
.
Продолжаем расправляться с функциями начала урока:
Пример 10
Построить график функции 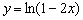
Представим функцию в виде 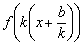 . В данном случае:
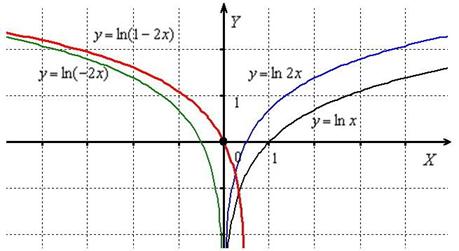
. В данном случае: 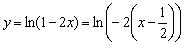 Построение проведём в три шага. График натурального логарифма
Построение проведём в три шага. График натурального логарифма 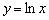 :
:
1) сожмём к оси 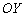 в 2 раза:
в 2 раза: 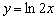 ;
;
2) отобразим симметрично относительно оси 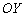 :
: 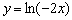 ;
;
3) сдвинем вдоль оси 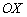 на
на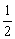 (!!!) вправо:
(!!!) вправо: 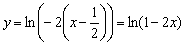 :
:
Для самоконтроля в итоговую функцию 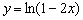 можно подставить пару значений «икс», например,
можно подставить пару значений «икс», например, 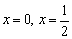 и свериться с полученным графиком.
и свериться с полученным графиком.
В рассмотренных параграфах события происходили «горизонтально» – гармонь играет, ноги пляшут влево/вправо. Но похожие преобразования происходят и в «вертикальном» направлении – вдоль оси 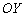 . Принципиальное отличие состоит в том, что связаны они не с АРГУМЕНТОМ, а с САМОЙ ФУНКЦИЕЙ.
. Принципиальное отличие состоит в том, что связаны они не с АРГУМЕНТОМ, а с САМОЙ ФУНКЦИЕЙ.
Растяжение (сжатие) графика ВДОЛЬ оси ординат.
Симметричное отображение графика относительно оси абсцисс
Структура второй части статьи будет очень похожа.
1) Если ФУНКЦИЯ 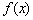 умножается на число
умножается на число 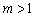 , то происходит растяжение её графика вдоль оси ординат.
, то происходит растяжение её графика вдоль оси ординат.
Правило: чтобы построить график функции 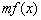 , где
, где 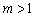 , нужно график функции
, нужно график функции 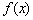 растянуть вдоль оси
растянуть вдоль оси 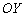 в
в 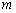 раз.
раз.
2) Если ФУНКЦИЯ умножается на число 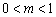 , то происходит сжатие её графика вдоль оси ординат.
, то происходит сжатие её графика вдоль оси ординат.
Правило: чтобы построить график функции 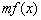 , где
, где 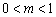 , нужно график функции
, нужно график функции 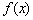 сжать вдоль оси
сжать вдоль оси 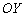 в
в 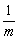 раз.
раз.
Догадайтесь, какую функцию я буду снова пытать =)
Пример 11
Построить графики функций 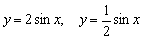 .
.
Берём синусоиду за макушку/пятки:
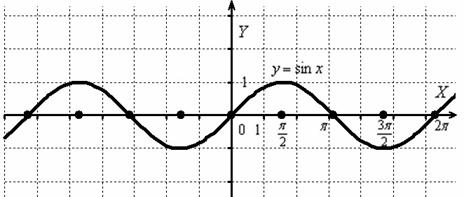
И вытягиваем её вдоль оси 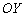 в 2 раза:
в 2 раза:
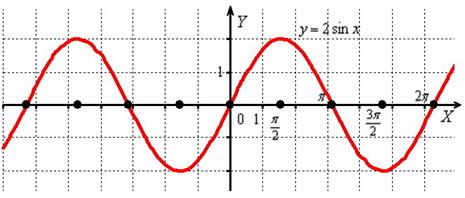
Период функции 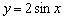 не изменился и составляет
не изменился и составляет 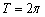 , а вот значения (все, кроме нулевых) увеличились по модулю в два раза, что логично – ведь функция умножается на 2, и область её значений удваивается:
, а вот значения (все, кроме нулевых) увеличились по модулю в два раза, что логично – ведь функция умножается на 2, и область её значений удваивается: 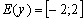 .
.
Теперь сожмём синусоиду вдоль оси 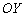 в 2 раза:
в 2 раза:
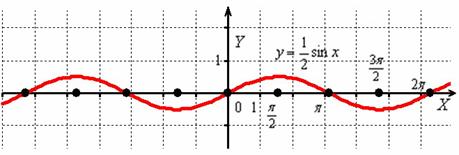
Аналогично, период 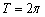 не изменился, но область значений функции «сплющилась» в два раза:
не изменился, но область значений функции «сплющилась» в два раза: 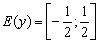 .
.
Нет, у меня нет какого-то пристрастного отношения к синусоиде, просто я хотел продемонстрировать, чем отличаются графики функций 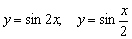 (Примеры №№1,3) от только что построенных собратьев
(Примеры №№1,3) от только что построенных собратьев 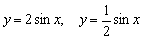 . Постарайтесь ещё раз проанализировать и качественнее понять эти элементарные случаи. Даже минимальные знания о преобразованиях графиков окажут вам неоценимую помощь в ходе решения других задач высшей математики!
. Постарайтесь ещё раз проанализировать и качественнее понять эти элементарные случаи. Даже минимальные знания о преобразованиях графиков окажут вам неоценимую помощь в ходе решения других задач высшей математики!
И, конечно же, классический пример растяжения/сжатия параболы:
Пример 12
Построить графики функций 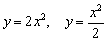 .
.
Возьмём рога молодого оленя 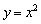 и вытянем их вверх вдоль оси
и вытянем их вверх вдоль оси 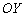 в два раза:
в два раза: 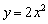 . Затем сожмём
. Затем сожмём 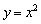 вдоль оси ординат в 2 раза:
вдоль оси ординат в 2 раза: 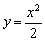
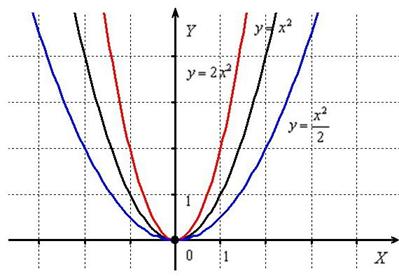
И снова заметьте, что значения функции 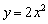 увеличиваются в 2 раза, а значения
увеличиваются в 2 раза, а значения 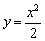 уменьшаются во столько же раз (исключение составляет точка
уменьшаются во столько же раз (исключение составляет точка 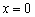 ).
).
Отпустим в тундру удивлённое животное и продолжим изучать умножение функции на число: 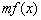 . Случаи
. Случаи 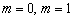 не представляют интереса, поэтому рассмотрим отрицательные коэффициенты. Сначала распространённый частный случай
не представляют интереса, поэтому рассмотрим отрицательные коэффициенты. Сначала распространённый частный случай 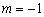 :
:
Если ФУНКЦИЯ меняет знакна противоположный, то её график отображается симметрично относительно оси абсцисс.
Правило: чтобы построить график функции 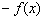 , нужно график
, нужно график 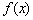 отобразить симметрично относительно оси
отобразить симметрично относительно оси 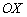 .
.
Пример 13
Построить график функции 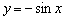
Отобразим синусоиду симметрично относительно оси 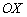 :
:
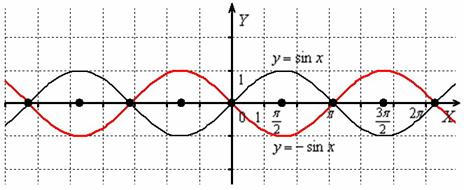
Ещё более наглядно симметрия просматривается у следующей типовой функции:
Пример 14
Построить график функции 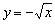
График функции 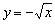 получается путём симметричного отображения графика
получается путём симметричного отображения графика 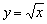 относительно оси абсцисс:
относительно оси абсцисс:
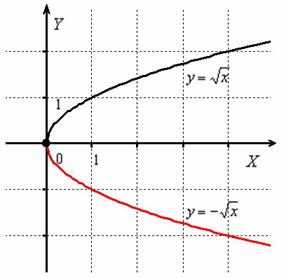
Функции 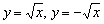 задают две ветви параболы, которая «лежит на боку». Обратная функция
задают две ветви параболы, которая «лежит на боку». Обратная функция 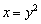 задаёт параболу целиком. С подобными графиками часто приходится иметь дело при нахождении площадей фигур, построении областей интегрирования двойных интегралов и в некоторых других задачах.
задаёт параболу целиком. С подобными графиками часто приходится иметь дело при нахождении площадей фигур, построении областей интегрирования двойных интегралов и в некоторых других задачах.
При умножении функции на отрицательное число 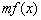 ,
, 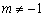 , построение графика следует выполнить в два этапа: сжатие (или растяжение) вдоль оси ординат, а потом – симметричное отображение относительно оси абсцисс. Конкретные примеры увидим в следующем топике.
, построение графика следует выполнить в два этапа: сжатие (или растяжение) вдоль оси ординат, а потом – симметричное отображение относительно оси абсцисс. Конкретные примеры увидим в следующем топике.
 2015-10-13
2015-10-13 100190
100190
