Задача Д5

Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3 — 6, прикрепленных к этим нитям, и невесомого блока (рис. Д5.0 — Д5.9, табл. Д5). Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом М, приложенной к одному из шкивов. Радиусы ступеней шкива 1 равны: 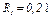, , 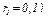а шкива 2 — 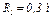, 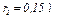; их радиусы инерции относительно осей вращения равны соответственно 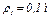и .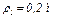

Пренебрегая трением, определить ускорение груза, имеющего больший вес; веса 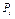,..., 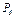шкивов и грузов заданы в таблице в ньютонах. Грузы, веса которых равны нулю, на чертеже не изображать (шкивы 1, 2 изображать всегда как части системы).

Указания. Задача Д5 — на применение к изучению движения системы общего уравнения динамики (принципа Даламбера — Лагранжа). Ход решения задачи такой же, как в задаче Д9, только предварительно надо присоединить к действующим на систему силам соответствующие силы инерции. Учесть при этом, что для однородного тела, вращающегося вокруг своей оси симметрии (шкива), система сил инерции приводится к паре с моментом 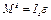, где 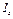— момент инерции тела относительно оси вращения, 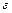— угловое ускорение тела; направление 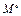противоположно направлению .

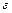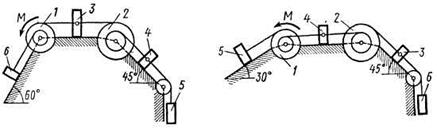
Рис. Д5.0 Рис. Д5.1

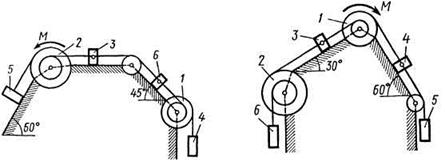
Рис. Д5.2 Рис. Д5.3

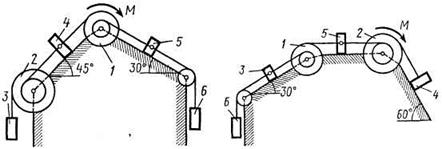
Рис. Д5.4 Рис. Д5.5

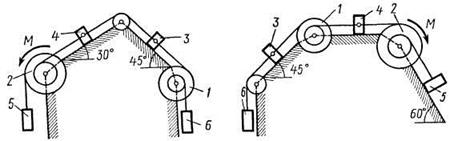
Рис. Д5.6 Рис. Д5.7

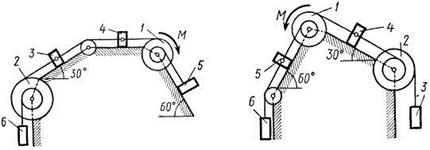
Рис. Д5.8 Рис. Д5.9

Таблица Д5

Номер условия	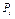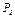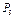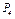, Н	, Н	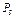, Н	, Н	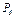, Н	, Н	М, Нм

Пример Д5. Механическая система (рис. Д5) состоит из обмотанных нитями блока 1 радиуса 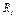и ступенчатого шкива 2 (радиусы ступене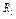й и 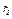, радиус инерции относительно оси вращения 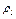), а также из грузов 3 и 4, прикрепленных к этим нитям.
Система движется в вертикальной плоскости под действием сил тяжести ипары сил с моментом М, приложенной к блоку 1.

Дано: , , , , , , , , .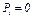

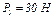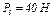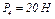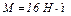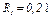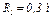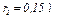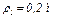Определить: ускорение груза 3, пренебрегая трением.

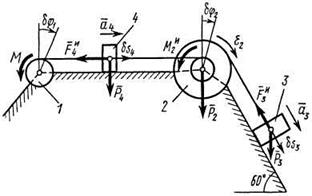
Рис. Д5

Решение. 1. Рассмотрим движение механической системы, состоящей из тел 1, 2, 3, 4, соединенных нитями. Система имеет одну степень свободы. Связи, наложенные на эту систему, — идеальные.

Для определения 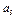применим общее уравнение динамики:

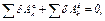(1)

где 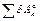— сумма элементарных работ активных сил; 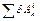— сумма элементарных работ сил инерции.

2. Изображаем на чертеже активные силы 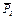, , 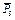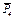и пару сил с моментом М. Задавшись направлением ускорения 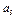, изображаем на чертеже силы инерции 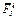, 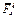и пару сил инерции с моментом 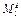, величины которых равны:

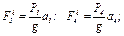
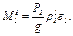(2)

3. Сообщая системе возможное перемещение и составляя уравнение (1), получим

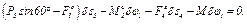(3)

Выразим все перемещения через :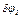

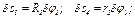
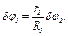(4)

Подставив величины (2) и (4) в уравнение (3), приведем его к виду

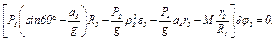(5)

Входящие сюда величины 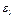и 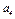выразим через искомую величину :

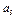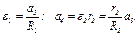
Затем, учтя, что 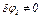, приравняем нулю выражение, стоящее в (5) в квадратных скобках.

Из полученного в результате уравнения найдем

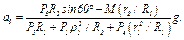
Вычисления дают следующий ответ: 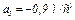. Знак указывает, что ускорение груза 3 и ускорения других тел направлены противоположно показанным на рис. Д5.