Механизм, расположенный в вертикальной плоскости (рис. Д6.0 — Д6.9), состоит из ступенчатых колес 1 и 2 с радиусами 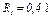 ,
, 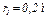 ,
, 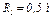 ,
, 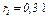 , имеющих неподвижные оси вращения; однородного стержня 3 длиной
, имеющих неподвижные оси вращения; однородного стержня 3 длиной 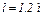 , закрепленного шарниром на одном из концов; грузов 4 и 5, подвешенных к нитям, намотанным на колеса. На стержне расстояние
, закрепленного шарниром на одном из концов; грузов 4 и 5, подвешенных к нитям, намотанным на колеса. На стержне расстояние 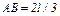 .
.
Таблица Д6
| Номер условия | 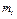 | 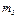 | 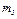 | 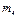 | 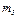 | 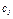 |  |  |
| — | — | — | — | |||||
| — | — | — | — | |||||
| — | — | — | — | |||||
| — | — | — | — | — | ||||
| — | — | — | — | — | ||||
| — | — | — | — | |||||
| — | — | — | — | |||||
| — | — | — | — | |||||
| — | — | — | — | |||||
| — | — | — | — |
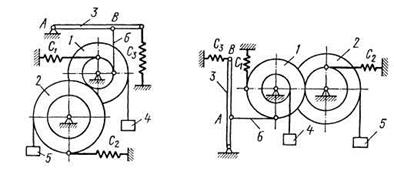
Рис. Д6.0 Рис. Д6.1
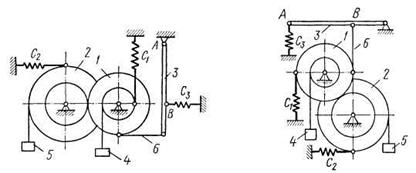
Рис. Д6.2 Рис. Д6.3
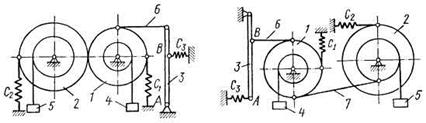
Рис. Д6.4 Рис. Д6.5
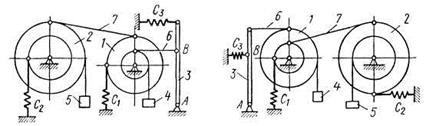
Рис. Д6.6 Рис. Д6.7
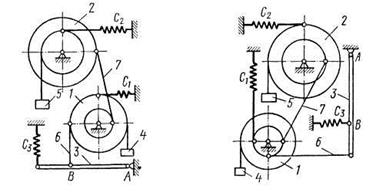
Рис. Д6.8 Рис. Д6.9
Стержень 3 соединен с колесом 2 невесомым стержнем 6. Колеса 1 и 2 или находятся в зацеплении (рис. 0 - 4), или соединены невесомым стержнем 7 (рис. 5 - 9). К колесам и стержню 3 прикреплены пружины.
В табл. Д6 заданы массы  тел (кг) и коэффициенты жесткости
тел (кг) и коэффициенты жесткости 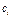 пружин (Н/м). Прочерки в столбцах таблицы означают, что соответствующие тела или пружины в систему не входят (на чертеже эти тела и пружины не изображать); в результате в каждом конкретном варианте получается довольно простой механизм, содержащий три или даже два тела. Стержень 6 или 7 входит всостав механизма, когда внего входят оба тела, соединенные этим стержнем.
пружин (Н/м). Прочерки в столбцах таблицы означают, что соответствующие тела или пружины в систему не входят (на чертеже эти тела и пружины не изображать); в результате в каждом конкретном варианте получается довольно простой механизм, содержащий три или даже два тела. Стержень 6 или 7 входит всостав механизма, когда внего входят оба тела, соединенные этим стержнем.
В положениях, изображенных на рисунках, механизм находится в равновесии. Определить частоту и период малых колебаний системы около положения равновесия. Найти также, чему равно статическое удлинение (сжатие) пружины 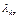 в положении равновесия.
в положении равновесия.
При подсчетах считать колеса 1 и 2 сплошными однородными цилиндрами радиусов 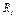 и
и 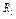 соответственно.
соответственно.
Рассмотрим два примера решения этой задачи.
Пример Д6а. Находящаяся в равновесии механическая система состоит из колеса 1 радиуса 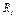 , ступенчатого колеса 2 с радиусами
, ступенчатого колеса 2 с радиусами 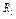 и
и 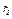 и груза 3, подвешенного на нити, намотанной на колесо 2; колеса соединены невесомым стержнем AВ (рис. Д6а). К колесу 1 прикреплена вертикальная пружина с коэффициентом жесткости с.
и груза 3, подвешенного на нити, намотанной на колесо 2; колеса соединены невесомым стержнем AВ (рис. Д6а). К колесу 1 прикреплена вертикальная пружина с коэффициентом жесткости с.
Дано: 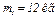 ,
, 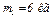 ,
, 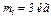 ,
, 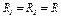 ,
, 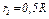 ,
, 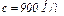 .
.
Колеса считать сплошными однородными цилиндрами.
Определить: частоту 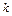 и период
и период 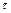 малых колебаний системы около положения равновесия и значение
малых колебаний системы около положения равновесия и значение 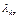 .
.
Решение. 1. Система имеет одну степень свободы. Выберем в качестве обобщенной координаты угол  поворота колеса 1 от равновесного положения (при равновесии
поворота колеса 1 от равновесного положения (при равновесии 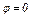 и
и 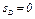 ,
, 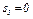 ) при движении системы, рассматривая малые колебания, считаем угол
) при движении системы, рассматривая малые колебания, считаем угол  малым.
малым.
Поскольку все действующие на систему активные силы потенциальные (сила тяжести и сила упругости), выразим обобщенную силу Q через потенциальную энергию П системы. Тогда исходным уравнением будет
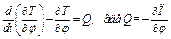 (1)
(1)
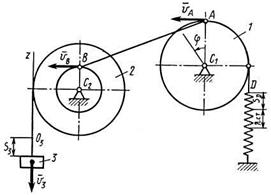
Рис.Д6а
2. Определим кинетическую энергию системы, равную сумме энергий всех тел:
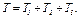 (2)
(2)
Так как колеса 1 и 2 вращаются вокруг осей  , и
, и  , а груз 3 движется поступательно, то
, а груз 3 движется поступательно, то
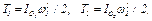
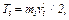 (3)
(3)
где
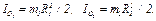 (4)
(4)
Все скорости, входящие в равенства (3), надо выразить через обобщенную скорость 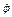 . Тогда
. Тогда 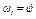 . Далее, ввиду малости угла
. Далее, ввиду малости угла  можно считать в каждый момент времени
можно считать в каждый момент времени 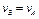 , т. е.
, т. е. 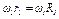 , откуда
, откуда 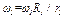 и
и 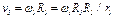 . Отсюда, учтя, что
. Отсюда, учтя, что 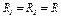 ,
, 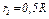 , получим
, получим
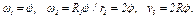 (5)
(5)
Подставляя величины (4), где 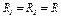 и (5) в равенства (3), получим из равенства (2)
и (5) в равенства (3), получим из равенства (2)
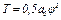 где
где 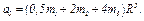 (6)
(6)
Отсюда находим
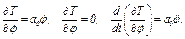 (7)
(7)
3. Определим потенциальную энергию П системы, учитывая, что для пружины 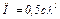 где
где 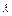 — удлинение (сжатие) пружины, а для поля сил тяжести
— удлинение (сжатие) пружины, а для поля сил тяжести 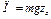 где
где 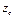 — координата центра тяжести (ось z направлена по вертикали вверх).
— координата центра тяжести (ось z направлена по вертикали вверх).
Тогда для всей системы
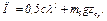 (8)
(8)
Определяя 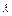 , учтем, что в положении равновесия пружина может иметь некоторое статическое (начальное) удлинение или сжатие
, учтем, что в положении равновесия пружина может иметь некоторое статическое (начальное) удлинение или сжатие 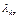 , необходимое для сохранения равновесия (в нашем случае для уравновешивания силы тяжести, действующей на груз 3). При повороте колеса 1 на угол
, необходимое для сохранения равновесия (в нашем случае для уравновешивания силы тяжести, действующей на груз 3). При повороте колеса 1 на угол  пружина получит дополнительное к
пружина получит дополнительное к 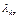 удлинение
удлинение 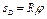 . Следовательно,
. Следовательно, 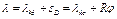 .
.
Для 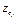 , направляя ось z из точки О3 вверх, получим
, направляя ось z из точки О3 вверх, получим 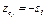 . Чтобы выразить
. Чтобы выразить 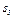 через
через  , заметим, что зависимость между малыми перемещениями здесь будет такой же, как между соответствующими скоростями. Тогда по аналогии с последним из равенств (5)
, заметим, что зависимость между малыми перемещениями здесь будет такой же, как между соответствующими скоростями. Тогда по аналогии с последним из равенств (5) 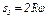 и
и 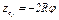 .
.
Подставляя все найденные величины в равенство (8), получим
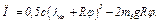 (9)
(9)
4. Определим обобщенную силу 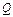 и
и 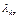 . Сначала находим
. Сначала находим
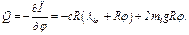 (10)
(10)
Входящую сюда неизвестную величину 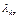 найдем из условия, что при равновесии, т.е. когда
найдем из условия, что при равновесии, т.е. когда 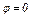 , должно быть и
, должно быть и 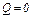 . Полагая в (10)
. Полагая в (10) 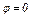 и
и 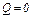 , получим
, получим 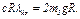 , откуда
, откуда
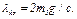 (11)
(11)
Заменяя в (10) 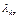 этим значением, найдем, что
этим значением, найдем, что
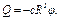 (12)
(12)
5. Составляем уравнение Лагранжа. Подставляя значения производных из равенств (7) и значение 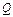 из (12) в уравнение (1), получим
из (12) в уравнение (1), получим 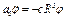 или, с учетом обозначения в (6),
или, с учетом обозначения в (6),
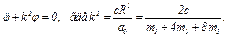 (13)
(13)
Из теории колебаний известно, что когда уравнение приведено к виду (13), то в нем 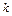 является искомой круговой частотой, а период колебаний
является искомой круговой частотой, а период колебаний 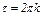 . При заданных числовых значениях
. При заданных числовых значениях 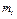 ,
, 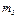 ,
, 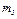 и
и 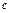 , произведя соответствующие подсчеты, получим из (13) и (11)
, произведя соответствующие подсчеты, получим из (13) и (11)
Ответы: 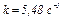 ,
, 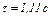 ,
, 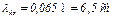 .
.
Пример Д6б. Находящаяся в равновесии механическая система состоит из однородного стержня 1, ступенчатого колеса 2 с радиусами ступеней R2 и r2 груза 3, подвешенного на нити, перекинутой через блок 4 и намотанной на колесо 2, и невесомого стержня 5, соединяющего тела 1 и 2 (рис. Д6, б ). В точке  шарнир; в точке А прикреплена горизонтальная пружина с коэффициентом жесткости с.
шарнир; в точке А прикреплена горизонтальная пружина с коэффициентом жесткости с.
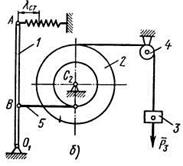
Рис.Д6,б
Дано: 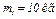 ,
, 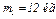 ,
, 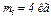 ,
, 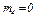 ,
, 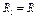 ,
, 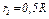 ,
, 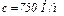 ,
, 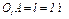 ,
, 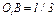 . Колесо 2 считать сплошным однородным цилиндром.
. Колесо 2 считать сплошным однородным цилиндром.
Определить: частоту 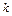 и период
и период 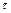 малых колебаний системы около положения равновесия и значение
малых колебаний системы около положения равновесия и значение 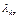 .
.
Решение. 1. Рассмотрим произвольное положение системы, когда она выведена из состояния равновесия и совершает малые колебания (рис. Д6, в). Система имеет одну степень свободы. Выберем в качестве обобщенной координаты угол  отклонения стержня от вертикали, считая
отклонения стержня от вертикали, считая  малым, и составим для системы уравнение Лагранжа. Поскольку все действующие активные силы (сила упругости и силы тяжести) потенциальные, выразим обобщенную силу
малым, и составим для системы уравнение Лагранжа. Поскольку все действующие активные силы (сила упругости и силы тяжести) потенциальные, выразим обобщенную силу 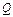 через потенциальную энергию П системы. Тогда исходным уравнением будет
через потенциальную энергию П системы. Тогда исходным уравнением будет
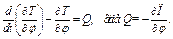 (1)
(1)
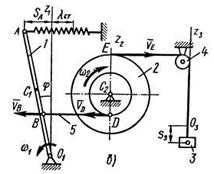
Рис.Д6, в
При исследовании малых колебаний в уравнении сохраняют малые величины  ,
, 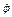 в первой степени, отбрасывая малые более высокого порядка. Для этого надо найти выражения Т и П с точностью до
в первой степени, отбрасывая малые более высокого порядка. Для этого надо найти выражения Т и П с точностью до 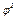 и
и 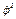 , так как в (1) входят первые производные от Т и П по
, так как в (1) входят первые производные от Т и П по  и
и 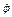 , а при дифференцировании многочлена его степень понижается на единицу
, а при дифференцировании многочлена его степень понижается на единицу
2. Определим кинетическую энергию Т системы, равную сумме энергий всех тел:
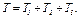 (2)
(2)
Так как стержень 1 и колесо 2 вращаются вокруг осей 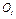 и
и 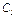 соответственно, а груз 3 движется поступательно, то
соответственно, а груз 3 движется поступательно, то
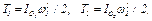
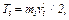 (3)
(3)
где
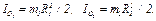 (4)
(4)
Все скорости, входящие в равенства (3), надо выразить через обобщенную скорость 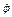 . Тогда
. Тогда 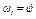 . Затем ввиду малости
. Затем ввиду малости  можно считать
можно считать 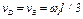 . Учтя это, найдем
. Учтя это, найдем 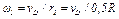 и
и 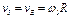 .Таким образом,
.Таким образом, 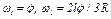 ;
;
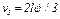 (5)
(5)
Подставляя величины (4) и (5) в равенства (3), получим из (2)
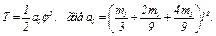 (6)
(6)
Отсюда находим
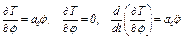 (7)
(7)
3. Определим потенциальную энергию П системы, учитывая, что для пружины 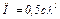 , где
, где 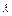 — удлинение (сжатие) пружины, а для поля сил тяжести
— удлинение (сжатие) пружины, а для поля сил тяжести 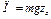 , где
, где 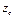 — координата центра тяжести (ось z направлена по вертикали вверх). Тогда для всей системы
— координата центра тяжести (ось z направлена по вертикали вверх). Тогда для всей системы
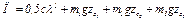 (8)
(8)
где величины 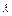 ,
, 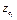 ,
, 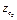 ,
, 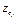 должны быть выражены через
должны быть выражены через  .
.
Определяя 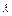 учтем, что в положении равновесия пружина может иметь некоторое статическое (начальное) удлинение или сжатие
учтем, что в положении равновесия пружина может иметь некоторое статическое (начальное) удлинение или сжатие 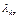 , необходимое для сохранения равновесия (в нашем случае для уравновешивания силы тяжести
, необходимое для сохранения равновесия (в нашем случае для уравновешивания силы тяжести 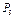 ). В произвольном положении (см. рис. Д6, в ) пружина получит дополнительное удлинение, равное
). В произвольном положении (см. рис. Д6, в ) пружина получит дополнительное удлинение, равное 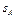 , причем ввиду малости
, причем ввиду малости  можно считать
можно считать 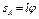 . Тогда
. Тогда 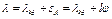
Для 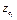 направляя ось
направляя ось 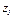 из точки
из точки 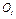 вверх, получим
вверх, получим 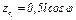 . Разлагая здесь
. Разлагая здесь 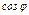 в ряд и сохраняя член с
в ряд и сохраняя член с 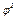 , получим[2]
, получим[2]
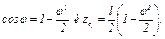
Для 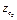 , взяв начало координат в точке
, взяв начало координат в точке  получим
получим 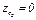 .
.
Для 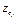 совмещая начало координат
совмещая начало координат 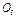 с положением центра тяжести груза 3 при равновесии, получим
с положением центра тяжести груза 3 при равновесии, получим 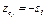 , где
, где 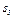 — перемещение груза. Чтобы выразить
— перемещение груза. Чтобы выразить 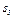 через
через  , заметим, что зависимость между малыми перемещениями здесь будет такой же, как между соответствующими скоростями. Тогда по аналогии с последним из равенств (5)
, заметим, что зависимость между малыми перемещениями здесь будет такой же, как между соответствующими скоростями. Тогда по аналогии с последним из равенств (5) 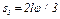 и
и 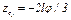 .
.
Подставляя все найденные величины в равенство (8), получим
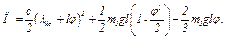 (9)
(9)
4. Определим обобщенную силу 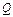 и
и 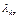 . Сначала находим
. Сначала находим
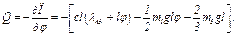 (10)
(10)
Входящую сюда неизвестную величину 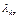 найдем из условия, что при равновесии, т.е. когда
найдем из условия, что при равновесии, т.е. когда 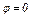 , должно быть и
, должно быть и 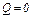 . Полагая в равенстве (10)
. Полагая в равенстве (10) 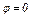 и
и 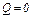 , получим
, получим 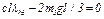 , откуда
, откуда
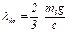 (11)
(11)
Заменяя в (10) 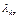 этим значением, найдем окончательно
этим значением, найдем окончательно
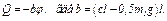 (12)
(12)
5. Составляем уравнение Лагранжа. Подставив значения производных из равенств (7) и значение 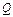 из (12) в уравнение (1), получим
из (12) в уравнение (1), получим 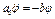 или
или
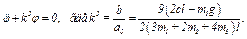 (13)
(13)
Из теории колебаний известно, что когда уравнение приведено к виду (13), то в нем величина 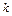 является искомой круговой частотой, а период
является искомой круговой частотой, а период 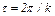 . При заданных числовых значениях, произведя соответствующие расчеты, получим из (13) и (11) следующие ответы:
. При заданных числовых значениях, произведя соответствующие расчеты, получим из (13) и (11) следующие ответы: 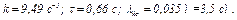
Другое решение. Рассмотрим другой путь решения задачи, пригодный и когда действующие силы не потенциальны.
Выберем опять в качестве обобщенной координаты угол  , считая его малым, и составим для системы уравнение Лагранжа
, считая его малым, и составим для системы уравнение Лагранжа
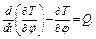 (14)
(14)
Для кинетической энергии Т системы и для соответствующих производных получим, как и раньше, значения (6) и (7).
Чтобы найти обобщенную силу 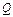 , надо изобразить на чертеже (рис. Д6, б) действующие активные силы, совершающие работу при перемещении системы, т.е. силу упругости пружины
, надо изобразить на чертеже (рис. Д6, б) действующие активные силы, совершающие работу при перемещении системы, т.е. силу упругости пружины 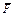 , приложенную к стержню 1 в точке А и направленную вправо (пружину считаем растянутой), силу тяжести
, приложенную к стержню 1 в точке А и направленную вправо (пружину считаем растянутой), силу тяжести 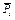 , приложенную к стержню 1 в точке
, приложенную к стержню 1 в точке 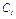 , и силу тяжести
, и силу тяжести 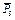 , приложенную к грузу 3; обе эти силы направлены по вертикали вниз (на рис. Д6, б силы
, приложенную к грузу 3; обе эти силы направлены по вертикали вниз (на рис. Д6, б силы 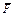 ,
, 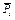 ,
, 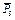 не показаны, но при решении задачи таким путем их надо изображать).
не показаны, но при решении задачи таким путем их надо изображать).
Теперь сообщаем системе возможное перемещение, при котором угол  получает положительное приращение
получает положительное приращение 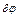 , и вычисляем работу
, и вычисляем работу 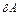 всех названных сил на этом перемещении. Получим
всех названных сил на этом перемещении. Получим
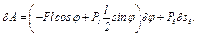 (15)
(15)
В равенстве (15) надо выразить 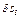 через
через 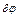 . По аналогии с последним из равенств (5) найдем, что
. По аналогии с последним из равенств (5) найдем, что
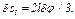 (16)
(16)
Определим еще значение силы упругости 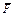 . По модулю
. По модулю 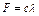 , где
, где 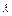 — удлинение пружины, слагающееся из начального удлинения
— удлинение пружины, слагающееся из начального удлинения 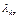 и дополнительного удлинения
и дополнительного удлинения 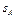 , которое ввиду малости угла
, которое ввиду малости угла  можно считать равным
можно считать равным 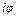 . Тогда
. Тогда 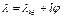 и
и
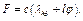 (17)
(17)
Подставив величины (16) и (17) в равенство (15) и учтя, что 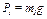 , а
, а 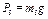 и что ввиду малости
и что ввиду малости  можно считать
можно считать 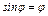 ,
, 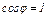 приведем окончательно равенство (15) к виду
приведем окончательно равенство (15) к виду
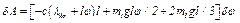
Коэффициент при 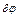 в правой части полученного равенства и является искомой обобщенной силой. Следовательно,
в правой части полученного равенства и является искомой обобщенной силой. Следовательно,
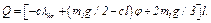 (18)
(18)
Величину 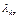 опять находим учитывая, что при равновесии, т.е. при
опять находим учитывая, что при равновесии, т.е. при 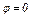 будет и
будет и 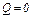 . В результате получим для
. В результате получим для 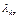 значение, даваемое формулой (11). При таком
значение, даваемое формулой (11). При таком 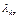 найдем из (18) окончательно, что
найдем из (18) окончательно, что
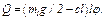 (19)
(19)
Подставляя значения соответствующих производных из равенств (7) и значение 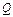 , даваемое формулой (19), в уравнение (14), приведем его окончательно к виду
, даваемое формулой (19), в уравнение (14), приведем его окончательно к виду
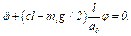 (20)
(20)
Решение уравнения (20) существенно зависит от знака коэффициента при  . Если этот коэффициент положителен, т. е.
. Если этот коэффициент положителен, т. е.
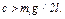 (21)
(21)
то, введя обозначение
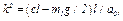 (22)
(22)
получим, как известно, решение уравнения (20) в вид
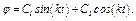 (23)
(23)
Если при 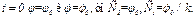 Но
Но 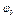 и
и 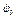 всегда можно выбрать столь малыми, что угол
всегда можно выбрать столь малыми, что угол  во все время движения тоже будет оставаться малым и, следовательно, система будет совершать малые колебания около положения ее равновесия, определяемого углом
во все время движения тоже будет оставаться малым и, следовательно, система будет совершать малые колебания около положения ее равновесия, определяемого углом 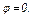 Равновесие системы в таком случае называют устойчивым; условие устойчивости равновесия определяется в данной задаче неравенством (21).
Равновесие системы в таком случае называют устойчивым; условие устойчивости равновесия определяется в данной задаче неравенством (21).
Если же коэффициент при  в уравнении (20) будет отрицательным, т.е. будет
в уравнении (20) будет отрицательным, т.е. будет 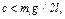 то введя обозначение
то введя обозначение 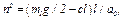 приведем уравнение (20) к виду
приведем уравнение (20) к виду 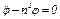 . Решением этого уравнения, как тоже известно, будет
. Решением этого уравнения, как тоже известно, будет
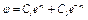
и, каковы бы ни были начальные условия, множитель 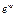 , а с ним и угол
, а с ним и угол  , будут со временем возрастать, т.е. система, выведенная из равновесного положения сколь угодно малым смещением (толчком), будет от этого положения все больше и больше отклоняться. Равновесие системы в таком случае называется неустойчивым.
, будут со временем возрастать, т.е. система, выведенная из равновесного положения сколь угодно малым смещением (толчком), будет от этого положения все больше и больше отклоняться. Равновесие системы в таком случае называется неустойчивым.
В решаемой задаче с = 750 Н/м, а 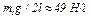 и неравенство (21) выполняется. Следовательно, равновесие системы является устойчивым и она может совершать около положения равновесия малые колебания. Круговая частота
и неравенство (21) выполняется. Следовательно, равновесие системы является устойчивым и она может совершать около положения равновесия малые колебания. Круговая частота 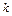 этих колебаний определяется из равенства (22), а период
этих колебаний определяется из равенства (22), а период 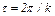 . Числовые значения искомых величин получаются, конечно, те же, что и в п. 5.
. Числовые значения искомых величин получаются, конечно, те же, что и в п. 5.
СПИСОК ЛИТЕРАТУРЫ
1. Тарг С.М. Краткий курс теоретической механики: Учебник для втузов. – 10 изд., пер. и доп. – М.: Высшая шк., 1986. – 416 с.
2. Теоретическая механика: Методические указания и контрольные задания для
студентов-заочников машиностроительных, строительных, транспортных, приборостроительных специальностей высших учебных заведений / Л.И. Котова, Р.И. Надеева, С.М. Тарг и др.; Под ред. С.М. Тарга// 4-е изд. М.: Высш. шк., 1989. -111 с.: ил.
3. Павловський М.А., Акинфиева Л.Ю., Бойчук О.Ф. Теоретическая механика. Статика. Кинематика. – К.: Вища шк. Головное изд-во, 1989. – 351 с.
4. Теоретическая механика. Динамика: Учебник/ М.А. Павловський, Л.Ю. Акинфиева, О.Ф. Бойчук; Под общ. ред. М.А. Павловского.– К.: Вища шк., 1990. – 480 с.
5. Добронравов В.В., Никитин Н.Н., Дворников А.Л. Курс теоретической механики. – М.:Высш.шк., 1974. – 528 с.
6. Мещерский И.В. Сборник задач по теоретической механике: Учебное пособие.- 36-е изд. – М.: Наука, 1986. – 448 с.
7. Сборник заданий для курсовых работ по теоретической механике: Учебн.пособие для техн. вузов/ Яблонский А.А., Норейко С.С., Вольфсон С.А. и др.; Под ред. А.А. Яблонского.- 4-е изд., перераб. и доп. М.: Высш. шк., 1985. - 367 с.
 2015-10-13
2015-10-13 1131
1131








