Механическая система состоит из прямоугольной вертикальной плиты 1 массой 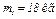 , движущейся вдоль горизонтальных направляющих, и груза D массой
, движущейся вдоль горизонтальных направляющих, и груза D массой 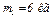 (рис. Д2.0 — Д2.9, табл. Д2). В момент времени
(рис. Д2.0 — Д2.9, табл. Д2). В момент времени 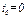 , когда скорость плиты
, когда скорость плиты 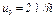 , груз под действием внутренних сил начинает двигаться по желобу плиты.
, груз под действием внутренних сил начинает двигаться по желобу плиты.
На рис. 0 - 3 желоб КЕ прямолинейный и при движении груза расстояние 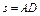 изменяется по закону
изменяется по закону 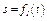 , а на рис. 4 - 9 желоб — окружность радиуса
, а на рис. 4 - 9 желоб — окружность радиуса 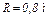 и при движении груза угол
и при движении груза угол 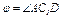 изменяется по закону
изменяется по закону 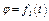 . В табл. Д2 эти зависимости даны отдельно для рис. 0 и 1, для рис. 2 и 3 и т. д., где
. В табл. Д2 эти зависимости даны отдельно для рис. 0 и 1, для рис. 2 и 3 и т. д., где 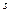 выражено в метрах,
выражено в метрах,  — в радианах,
— в радианах, 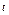 — в секундах.
— в секундах.
Считая груз материальной точкой и пренебрегая всеми сопротивлениями, определить зависимость 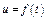 , т.е.скорость плиты как функцию времени.
, т.е.скорость плиты как функцию времени.
Таблица Д2
| Номер условия | 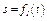 | 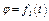 | ||
| рис. 0, 1 | рис. 2, 3 | рис. 4, 5, 6 | рис. 7, 8, 9 | |
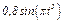 | 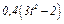 | 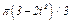 | 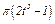 | |
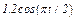 | 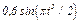 | 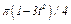 | 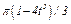 | |
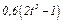 | 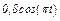 | 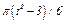 | 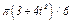 | |
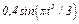 | 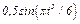 | 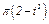 | 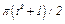 | |
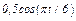 | 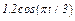 | 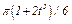 | 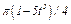 | |
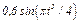 | 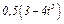 | 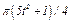 | 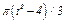 | |
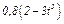 | 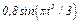 | 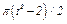 | 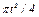 | |
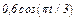 | 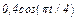 | 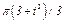 | 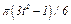 | |
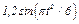 | 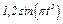 | 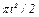 | 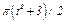 | |
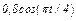 | 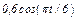 | 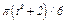 |  |
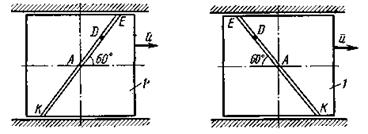
Рис. Д2.0 Рис. Д2.1
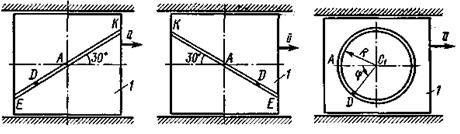
Рис. Д2.2 Рис. Д2.3 Рис.Д2.4
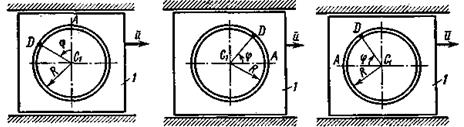
Рис. Д2.5 Рис. Д2.6 Рис.Д2.7
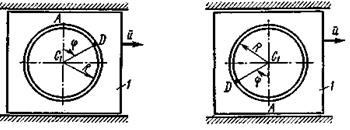
Рис. Д2.8 Рис. Д2.9
Указания. Задача Д2 на применение теоремы об изменении количества движения системы. При решении составить уравнение, выражающее теорему, в проекции на горизонтальную ось.
Пример Д2. В центре тяжести А тележки массой 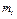 , движущейся по гладкой горизонтальной плоскости, укреплен невесомый стержень АD длиной l с грузом D массой
, движущейся по гладкой горизонтальной плоскости, укреплен невесомый стержень АD длиной l с грузом D массой 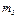 на конце (рис. Д2). В момент времени
на конце (рис. Д2). В момент времени 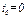 , когда скорость тележки
, когда скорость тележки 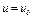 , стержень АD начинает вращаться вокруг оси А по закону
, стержень АD начинает вращаться вокруг оси А по закону 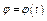 .
.
Дано: 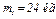 ,
, 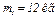 ,
, 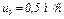 ,
, 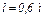 ,
, 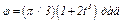
(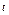 - в секундах).
- в секундах).
Определить: 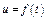 — закон изменения скорости тележки.
— закон изменения скорости тележки.
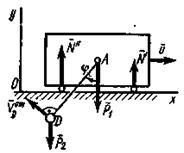
Рис. Д2
Решение. Рассмотрим механическую систему, состоящую из тележки и груза D, в произвольном положении. Изобразим действующие на систему внешние силы: силы
тяжести 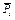 ,
, 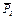 и реакции плоскости
и реакции плоскости 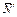 ,
, 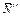 . Проведем координатные оси Оху так,чтобы ось х была горизонтальна.
. Проведем координатные оси Оху так,чтобы ось х была горизонтальна.
Чтобы определить и, воспользуемся теоремой об изменении количества движения системы 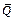 в проекции на ось х. Так как все действующие на систему внешние силы вертикальны (рис. Д2), то
в проекции на ось х. Так как все действующие на систему внешние силы вертикальны (рис. Д2), то 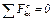 и теорема дает
и теорема дает
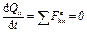 , откуда
, откуда 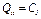 . (1)
. (1)
Для рассматриваемой механической системы 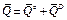 , где
, где 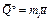 и
и 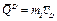 - количества движения тележки и груза D соответственно (
- количества движения тележки и груза D соответственно (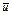 - скорость
- скорость
тележки, 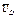 - скорость груза по отношению к осям Оху). Тогда из равенства (1) следует, что
- скорость груза по отношению к осям Оху). Тогда из равенства (1) следует, что
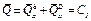 или
или 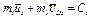 (2)
(2)
Для определения 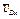 рассмотрим движение груза D как сложное, считая его движение по отношению к тележке относительным (это движение, совершаемое при вращении стержня АD вокруг оси А), а движение самой тележки — переносным. Тогда
рассмотрим движение груза D как сложное, считая его движение по отношению к тележке относительным (это движение, совершаемое при вращении стержня АD вокруг оси А), а движение самой тележки — переносным. Тогда 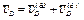 и
и
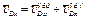 . (3)
. (3)
Но 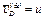 и, следовательно,
и, следовательно, 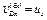 . Вектор
. Вектор 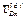 направлен перпендикулярно стержню и численно
направлен перпендикулярно стержню и численно 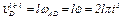 .
.
Изобразив этот вектор на рис. Д4 с учетом знака 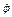 , найдем, что
, найдем, что 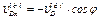 . Окончательно из равенства (3) получим
. Окончательно из равенства (3) получим
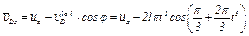 . (4)
. (4)
(В данной задаче величину 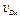 можно еще найти другим путем, определив абсциссу
можно еще найти другим путем, определив абсциссу 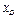 груза D, для которой, как видно из рис. Д4, получим
груза D, для которой, как видно из рис. Д4, получим 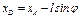 ; тогда
; тогда 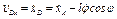 , где
, где 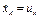 , а
, а 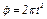 .)
.)
При найденном значении 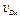 равенство (2), если учесть, что
равенство (2), если учесть, что 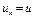 , примет вид
, примет вид
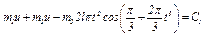 . (5)
. (5)
Постоянную интегрирования 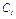 определим по начальным условиям: при
определим по начальным условиям: при 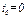 и
и 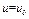 . Подстановка этих величин в уравнение (5) дает
. Подстановка этих величин в уравнение (5) дает 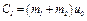 и тогда из (5) получим
и тогда из (5) получим
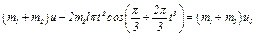 .
.
Отсюда находим следующую зависимость скорости 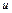 тележки от времени:
тележки от времени:
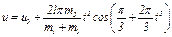 . (6)
. (6)
Подставив сюда значения соответствующих величин, находим искомую зависимость 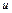 от
от 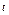 .
.
Ответ: 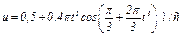 .
.
 2015-10-13
2015-10-13 738
738








