Основные уравнения

Уравнение теплового баланса. Для определённости далее будем считать, что индекс ₁ относится к характеристикам горячего теплоносителя, а индекс ₂ – холодного, причем теплоноситель ₁ – основной. Условие теплового баланса для них записывается в виде

,

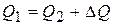где 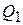– теплота, отдаваемая теплоносителем ₁, Вт,

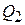– теплота, воспринимаемая теплоносителем ₂, Вт,

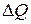– потери теплоты в окружающую среду.

Очевидно, ,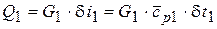

,

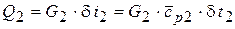где для каждого теплоносителя

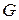– массовый расход, кг/с,

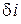– изменение удельной энтальпии теплоносителя в аппарате, Дж/кг,

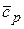– средняя удельная теплоёмкость теплоносителя, Дж/(кг·К),

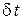– изменение температуры теплоносителя в аппарате, Дж/кг, , .

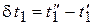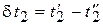Далее для простоты будем пренебрегать потерями теплоты 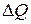, принимая 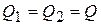. Для расчётов удобно ввести величину 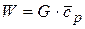, Вт/К. Она называется расходная теплоёмкость или полная теплоёмкость массового расхода (иногда её называют водяным эквивалентом). Тогда уравнение теплового баланса (то есть сохранения тепловой энергии) можно записать в форме

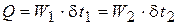. (1)

По (1) видно, что если один теплоноситель имеет намного бóльшую расходную теплоёмкость 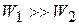, то изменение его температуры будет небольшим .

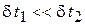Это соотношение справедливо не только для аппарата в целом, но и для любого элемента 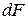его поверхности (рис.)

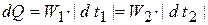, (1э)

где 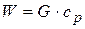, 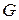– расход теплоносителя через элемент.

Уравнение теплопередачи. Теплопередача – обмен теплотой между двумя жидкостями (теплоносителями) через разделяющую их стенку – как раз и имеет место в рассматриваемых рекуперативных ТА. Ранее при изучении тепловодности через стенку для теплопередачи была получена формула 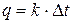, где обозначалось 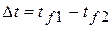– температурный напор, разность температур 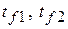жидкостей, 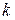– коэффициент теплопередачи. 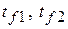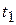Здесь температуры теплоносителей уже основные, и обозначаются не , а и 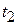, поэтому теперь температурный напор 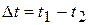. Тогда тепловой поток через элемент 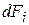рабочей поверхности запишется

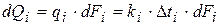. (2э)

В разных элементах ТА эти величины могут различаться, и всего в ТА 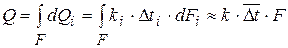. То есть можно принять за уравнение теплопередачи

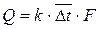, (2)

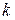где и 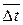– осреднённые по 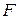значения локальных 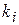и .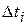

Можно отметить, что если уравнение баланса (1) выражает лишь условие сохранения тепловой энергии и, по существу, не связано непосредственно с устройством аппарата, то уравнение теплопередачи (2) учитывает организацию теплообменных процессов в ТА через , , .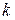

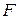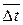Для расчёта температур по уравнениям (1), (2) нужно уметь определять значения 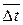и .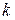

Средний температурный напор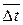

Прямоточные ТА. Рассмотрим характер изменения вдоль аппарата температур 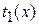, 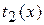и, следовательно, их разности – температурного напора 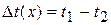(рис.). Пусть на входе в элемент 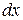аппарата напор равен 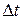, а на выходе – 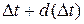. Как ясно из рисунка 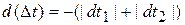, или, с учётом (1э), 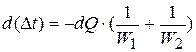. По (2э) 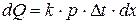, считая 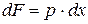( 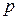– периметр сечения элемента), тогда

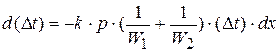. (3)

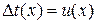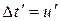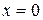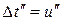Для наглядности будем при выкладках обозначать , соответственно, (при ), (при 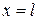). Пусть 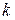и 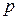не меняются по длине аппарата. При этом уравнение (3) запишется в ви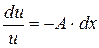де , где 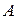– известная постоянная

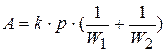. (4)

Решение этого уравнения (аналогично (Т26) в лекции о вынужденной конвекции в трубе) имеет вид

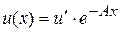, (5)

Откуда при 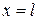получаем

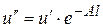(6)

или

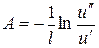. (7)

По (5) можно найти среднее значение

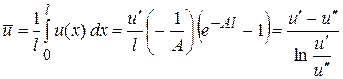(формула осреднения экспоненци­альной функции). Возвращаясь к прежнему обозначению 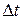, вновь получаем выражение для среднелогарифмического напора, аналогичное (Т2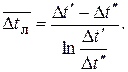8)

(8)

Здесь для прямоточных ТА

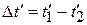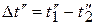, . (9_прям)

Подстановкой (4) в (6) с учётом 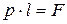получаем

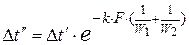. (10_прям)

Противоточные ТА. Здесь графики распределения температур имеют иной вид (рис.). Видно, что здесь 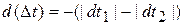, и по (1э) 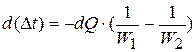. Далее все выкладки повторяются, как в предыдущем пункте, кроме минуса (вместо плюса) в (4), и приводят также к (8), где, однако, теперь вместо (9_прям) и (10_прям) будет

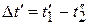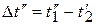, , (9_прот)

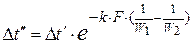. (10_прот)

Замечания. 1. Как и в случае формул (Т28) и (Т29), логарифмическое среднее 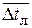по (8) близко к арифметическому 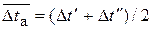при 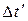близком к 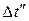, поэтому при 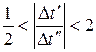в качестве 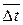в (2) вместо 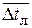по (8) считается возможным использовать более простое 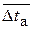. Но надо иметь в виду, что в случае противотока возможен случай 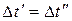, когда значение 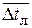по (8) вообще не определено. То есть при 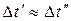следует использовать именно 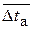, а не !

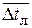2. Выражение (8) построено точными выкладками, но, как указывалось, в предположении 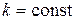. Обычно это близко к реальности, и использование (8) в (2) для прямоточных и противоточных ТА даёт вполне достаточную точность.

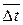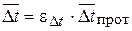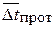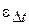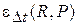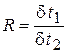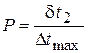ТА с другими схемами тока. В случае ТА с перекрёстным током или с многоходовыми, комбинированными и т.п. схемами аналитические построения сложны. При простых расчётах “вручную” для используют формулу , где определяют по формулам (8), (9_прот), а поправка даётся в справочниках как функция двух аргументов и , где .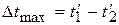

Коэффициент теплопередачи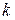

Коэффициент теплопередачи 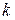определяется по формулам для соответствующих стенок (лекции прошлого семестра). Так, для плоских стенок (пластинчатые теплообменники)

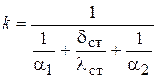(к1)

(для многослойных стенок, например, с учётом отложений и загрязнений, вместо 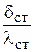подставляют ).

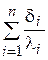Для трубчатых теплообменников в изложенном ранее материале (Ц20), (Ц22) использовался линейный коэффициент теплопередачи

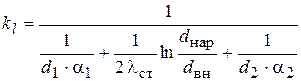. (к2)

Так как при этом по (Ц22) 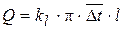(для одной трубки), то с учётом

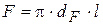(к3)

из сопоставления с (2) получаем выражение для 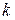через 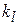для круглых труб

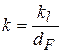. (к4)

Здесь 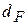– принимаемый диаметр теплообменной поверхности. При использовании (к2), (к4) можно брать .

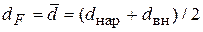Впрочем, обычно стенка трубки имеет высокую теплопроводность и толщину заметно меньше радиуса. Тогда, как показано ранее в (Ц30), (Ц31), и для трубок можно использовать простую формулу (к1) вместо более сложных (к2), (к4), если выбирать 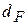по наибольшему термическому сопротивлению .

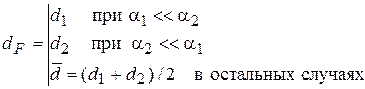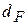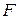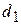На правильный выбор необходимо обращать внимание, так как, например, для трубки диаметром порядка 10 мм с толщиной стенки 1мм расчёт площади по вместо 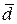(или наоборот) даст ошибку 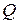порядка 10%, а по 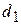вместо 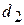– порядка 20%!

Далее остаётся учесть, что локальные значения коэффициента теплопередачи 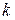меняются по ТА, хотя обычно не очень значительно. Для определения среднего значения можно применить разные подходы.

1) Расчёт ведётся непосредственно по (к1) [или (к2), (к4)], где в качестве 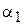, 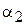берутся средние по поверхности 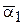, , 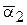рассчитываемые по соответствующим уравнениям подобия для 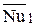, , 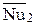в которых характеристики берутся для определяющих температур 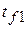, 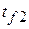– средних по аппарату. Если температура одного из теплоносителей 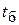меняется существенно нелинейно, то средняя температура другого берётся как средняя арифметическая 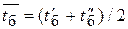, а этого – на основе среднелогарифмического температурного напора 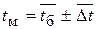(конкретный знак вместо ‘±’ – по логике процесса).

2) По второму способу вычисляются значения коэффициента теплопередачи на входе 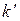и выходе 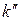и принимается 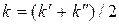. Достоинство этого способа – он позволяет попутно проверить, насколько сильно изменяется коэффициент теплопередачи в аппарате (обычно крайние значения находятся на концах). Если значения коэффициента теплопередачи в разных частях ТА заметно отличаются (например, из-за различия условий омывания поверхности), то теплообменную поверхность надо разделить на части, в пределах которых изменение достаточно мало, и рассчитывать их по отдельности (уравнение теплопередачи (2) справедливо только, если локальный коэффициент теплоотдачи близок к постоянной).

3) Точное уравнение теплопередачи, как ясно из вывода (2), должно иметь вид

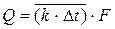, (2_точн)

где 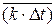– среднее по поверхности значение произведения локальных 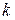и 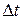. На этом основан третий способ, применимый, если распределение этого произведения по поверхности можно считать близким к экспоненциальному. При этом вместо средних 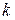и 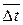по (к1) и (8) вычисляется среднелогарифмическое среднее произведения 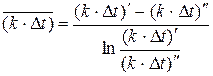и вместо (2) используется (2_точн). Впрочем, не при всех видах расчётов легко провести такую замену (см.ниже).