2015-10-13
786
Полагая, что генеральная совокупность Х имеет нормальное распределение, построим доверительный интервал для математического ожидания при неизвестном среднем квадратическом отклонении.
В курсе математической статистики доказывается, что случайная величина Т в случае выборки из нормальной совокупности, имеет распределение Стьюдента c (n –1)-й степенью свободы, не зависящее от параметров генеральной совокупности. Доверительный интервал с выбранной надежностью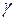 
, покрывающий математическое ожидание, будет иметь вид 
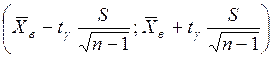. Для нахождения точности оценки 
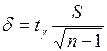значение 
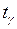определяется по таблице распределения Стьюдента по заданной надежности 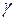и по числу степеней свободы k = (n – 1).
Построим 95% доверительный интервал для оценки математического ожидания. Тогда имеем 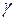= 0,95, число степеней свободы k = 51-1=50, уровень значимости α=1– 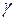=0,05. По таблице распределения Стъюдента находим 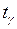=2,009. Точность оценки 
.
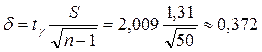Получаем доверительный интервал для оценки математического ожидания нормально распределенной генеральной совокупности:
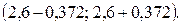Окончательно имеем (2,228; 2,972).
