Пусть имеются l нормально распределенных случайных величин 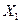 ,
, 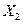 , …,
, …, 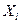 . По независимым выборкам, объемы которых равны
. По независимым выборкам, объемы которых равны 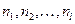 , найдены исправленные выборочные дисперсии
, найдены исправленные выборочные дисперсии 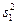 ,
,  , …,
, …, 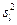 . Требуется при заданном уровне значимости a проверить основную гипотезу
. Требуется при заданном уровне значимости a проверить основную гипотезу 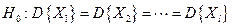 при конкурирующей гипотезе
при конкурирующей гипотезе 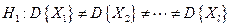 . Для проверки основной гипотезы
. Для проверки основной гипотезы 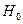 используют критерий Бартлетта.
используют критерий Бартлетта.
Порядок проверки:
1) находим наблюдаемое значение критерия по формуле
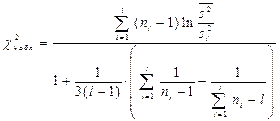 ,
,
где 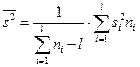 - оценка средней арифметической дисперсий случайных величин. Случайная величина
- оценка средней арифметической дисперсий случайных величин. Случайная величина 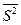 имеет
имеет 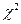 - распределение с
- распределение с 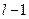 степенями свободы.
степенями свободы.
2) по таблице критических точек 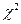 - распределения,по заданному уровню значимости a и числу степеней свободы
- распределения,по заданному уровню значимости a и числу степеней свободы 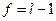 находим критическую точку
находим критическую точку 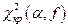 ;
;
3) если 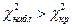 , то основную гипотезу
, то основную гипотезу 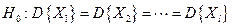 отвергаем в пользу конкурирующей гипотезы
отвергаем в пользу конкурирующей гипотезы 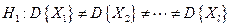 . Если
. Если 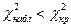 - нет оснований отвергнуть гипотезу
- нет оснований отвергнуть гипотезу 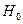 .
.
 2015-10-13
2015-10-13 1207
1207







