Проверка гипотезы о равенстве дисперсий нескольких нормально распределенных случайных величин. Критерий Кочрена

Пусть имеются l нормально распределенных случайных величин 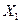, , 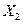…, 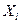. По независимым выборкам одинакового объема n (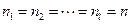) найдены исправленные выборочные дисперсии 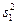, , …, 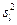. Требуется при заданном уровне значимости a проверить основную гипотезу о равенстве дисперсий l случайных величин 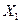, , 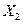…, 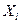при конкурирующей гипотезе об их неравенстве:

.

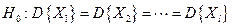
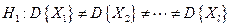Для проверки основной гипотезы 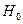используют критерий Кочрена.

Порядок проверки:

1) находим наблюдаемое значение критерия по формул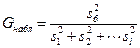е , где ;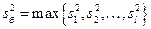

2) по таблице критических точек распределения Кочрена,по заданному уровню значимости a, по числу степеней свободы 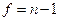и по числу l случайных величин 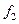находим критическую точку ;

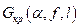3) если 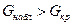, то основную гипотезу 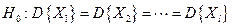отвергаем в пользу конкурирующей гипотезы 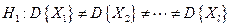. В этом случае говорят, что исправленные выборочные дисперсии 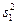, , …, 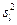различаются значимо или существенно. Их различие обусловлено действительным различием дисперсий случайных величин 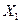, , 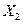…, 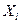. Если 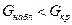- нет оснований отвергнуть гипотезу 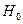. В этом случае говорят, что исправленные выборочные дисперсии 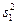, , …, 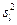различаются незначимо или несущественно. Их различие обусловлено случайностью выборки.