Пусть 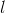 – некоторая кривая,
– некоторая кривая, 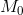 – точка на кривой
– точка на кривой 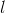 .
.
Любая прямая, пересекающая 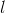 не менее чем в двух точках называется секущей.
не менее чем в двух точках называется секущей.
Касательной к кривой 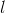 в точке
в точке 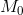 называется предельное положение секущей
называется предельное положение секущей 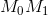 , если точка
, если точка 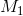 стремится к
стремится к 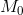 , двигаясь по кривой.
, двигаясь по кривой.
Из определения очевидно, что если касательная к кривой в точке 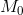 существует, то она единственная.
существует, то она единственная.
Рассмотрим кривую y = f(x) (т.е. график функции y = f(x)). Пусть в точке 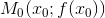 он имеет невертикальную касательную
он имеет невертикальную касательную 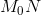 . Ее уравнение:
. Ее уравнение: 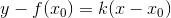 (уравнение прямой, проходящей через точку
(уравнение прямой, проходящей через точку 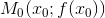 и имеющую угловой коэффициент k).
и имеющую угловой коэффициент k).
По определению углового коэффициента 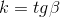 , где
, где 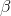 – угол наклона прямой
– угол наклона прямой 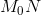 к оси
к оси 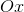 .
.
Пусть 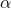 – угол наклона секущей
– угол наклона секущей 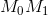 к оси
к оси 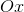 , где
, где 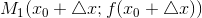 . Так как
. Так как 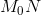 – касательная, то при
– касательная, то при 
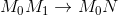 ⇒
⇒ 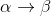 ⇒
⇒ 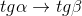 .
.
Следовательно,
Таким образом, получили, что 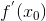 – это угловой коэффициент касательной к графику функции y = f(x) в точке
– это угловой коэффициент касательной к графику функции y = f(x) в точке 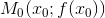 (геометрический смысл производной функции в точке). Поэтому уравнение касательной к кривой y = f(x) в точке
(геометрический смысл производной функции в точке). Поэтому уравнение касательной к кривой y = f(x) в точке 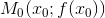 можно записать в виде
можно записать в виде
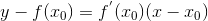
 2015-10-13
2015-10-13 331
331








