2015-10-13
340
Первообразная. Непрерывная функция F (x) называется первообразной для функции f (x) на промежутке X, если для каждого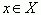 
F’ (x) = f (x).
П р и м е р. Функция F (x) = x 3 является первообразной для функции
f (x) = 3 x 2 на интервале (-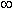 
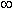, + ), так как
F’ (x) = (x 3) ’ = 3 x 2 = f (x) для всех x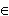 
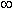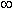(- , + ). Легко проверить, что функция x 3 + 13 имеет ту же производную 3 x 2, поэтому x 3 + 13 также является первообразной для функции 3 x 2 для всех x 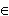(- 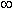, + 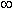). Ясно, что вместо 13 можно взять любую постоянную.
Таким образом, задача нахождения первообразной имеет бесчисленное множество решений. Этот факт нашёл отражение в определении неопределённого интеграла.
Неопределённый интеграл функции f (x) на промежутке X есть множество всех её первообразных. Это записывается в виде:
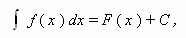
где C – любая постоянная, называемая постоянной интегрирования.
