Определённый интеграл. Формула Ньютона – Лейбница

Рассмотрим непрерывную функцию y = f (x), заданную на отрезке [ a, b ] и сохраняющую на этом отрезке свой знак (рис.8).
Фигура, ограниченная графиком этой функции, отрезком [ a, b ] и прямыми x = a и x = b, называется криволинейной трапецией.
Для вычисления площадей криволинейных трапеций используется следующая теорема:

Если f – непрерывная, неотрицательная функция на отрезке [a, b], и F – её первообразная на этом отрезке, то площадь соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a, b], т.e.

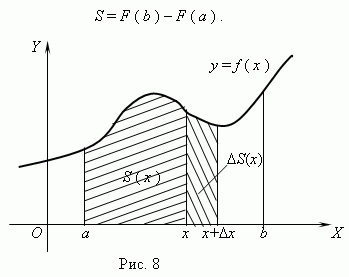
Рассмотрим функцию S (x), заданную на отрезке [ a, b ]. Если a<x 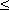b, то S (x) – площадь части криволинейной трапеции, лежащей слева от вертикальной прямой, проходящей через точку (x, 0). Отметим, что если x = a, то S (a) = 0, а S (b) = S (S – площадь всей криволинейной трапеции). Можно доказать, что

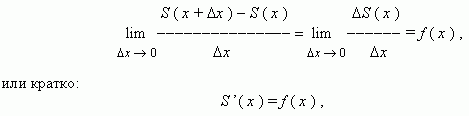
т.e. S (x) – первообразная для f (x). Отсюда, согласно основному свойству первообразных, для всех x 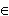[ a, b ] имеем:

S (x) = F (x) + C,

где C – некоторая постоянная, F – одна из первообразных функции f.

Чтобы найти C, подставим x = a:

F (a) + C = S (a) = 0,отсюда, C = - F (a) и S (x) = F (x) - F (a). Так как площадь криволинейной трапеции равна S (b), то подставляя x = b, получим: