Общее решение уравнений движения заряженной частицы в однородных и постоянных электрическом и магнитном полях в нерелятивистском приближении

В нерелятивистском приближении уравнения (5) сводятся к следующим уравнениям:

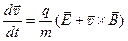. (6)

Их можно рассматривать в этом случае как систему линейных неоднородных дифференциальных уравнений первого порядка относительно вектора 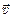, которой можно придать следующий вид:

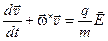, (7)

где вектор 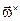– тензор, дуальный вектору 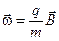. Общее решение соответствующей системы однородных уравнений 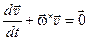можно записать в матричном виде

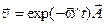, (8)

где 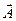– некоторый постоянный вектор. Тогда частное решение неоднородной системы (7) ищется в виде

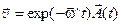. (9)

При подстановке (9) в (7) для векторной функции 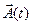имеем:

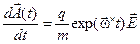. (10)

Для того, чтобы произвести интегрирование в (10), необходимо найти .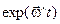

По определению,

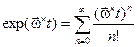. (11)

Так как тензор 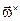удовлетворяет характеристическому уравнению

,

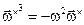то, вводя единичный вектор 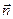, направленный вдоль вектора индукции магнитного поля, и группируя в правой части (11) слагаемые с четными и нечетными степенями, можно получить, что

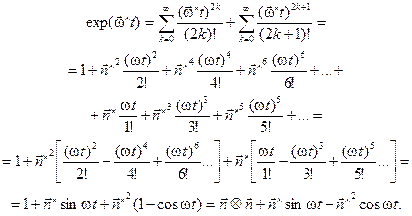(12)

Соответственно,

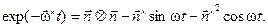(12')

Подставляя (12) в (10), можно найти векторную функцию :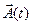

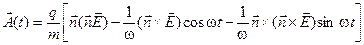. (13)

Тогда общее решение уравнения (7) с учетом (12') после некоторых преобразований запишется следующим образом:

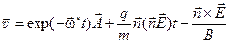. (14)

Второе начальное условие (3) позволяет определить постоянный вектор 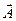. С учетом (12) будем иметь

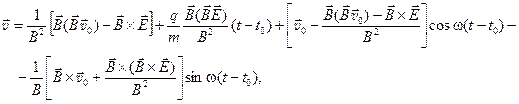(15)

где 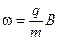– циклическая частота кругового движения нерелятивистской частицы в магнитном поле.

Интегрирование (15) по времени дает параметрическое уравнение траектории нерелятивистской частицы, движущейся в произвольных постоянных и однородных электрическом и магнитном полях:

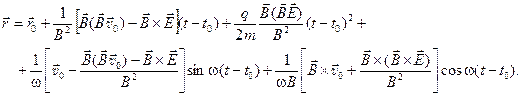(16)

Интерпретация этого общего решения (15), (16) зависит от конкретных начальных условий и взаимной ориентации векторов 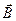и 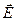. Тем не менее, из (15), (16) можно усмотреть, что в любом случае под действием электрического и магнитного полей происходит дрейф заряженной частицы с начальной скоростью 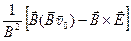и постоянным ускорением 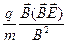с одновременным движением по окружности с циклической частотой w и радиусом

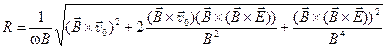. (17)

Т.е. траектория движения нерелятивистской заряженной частицы представляет собой круговую спираль, которая растягивается, либо сжимается в зависимости от направления векторов 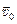, 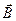и 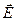, а также значения t – t ₀.