Пусть 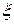 - корень уравнения
- корень уравнения 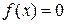 отделен на отрезке
отделен на отрезке 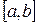 , причем
, причем 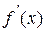 и
и 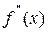 непрерывны и сохраняют определенные знаки на этом же отрезке
непрерывны и сохраняют определенные знаки на этом же отрезке 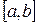 . Найдя какое-нибудь n-е значение корня
. Найдя какое-нибудь n-е значение корня 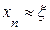 (
(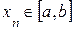 ), уточним его по методу Ньютона. Для этого положим
), уточним его по методу Ньютона. Для этого положим 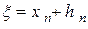 , где
, где 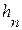 - считаем малой величиной. Разложим функцию f(x) в ряд Тейлора в окрестности точки x n по степеням h n. Тогда можно записать:
- считаем малой величиной. Разложим функцию f(x) в ряд Тейлора в окрестности точки x n по степеням h n. Тогда можно записать:
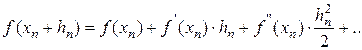
Ограничимся двумя членами ряда и так как 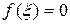 , то:
, то:
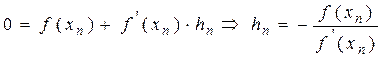 .
.
Учитывая найденную поправку hn:,получим 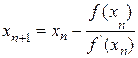 (n=0,1,2,…).
(n=0,1,2,…).
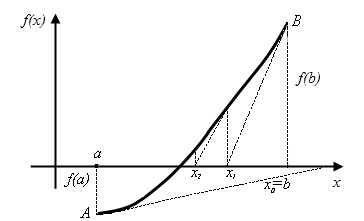
Рис.2.7 Метод касательных. Начальное приближение x0=b
По-другому этот метод называется методом касательных. Если в точке 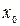 провести касательную к функции f(x), то ее пересечение с осью ОХ и будет новым приближением x1 корня уравнения
провести касательную к функции f(x), то ее пересечение с осью ОХ и будет новым приближением x1 корня уравнения
Хорошим начальным приближением 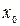 является то значение, для которого выполнено неравенство
является то значение, для которого выполнено неравенство 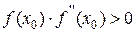 . Погрешность вычислений
. Погрешность вычислений 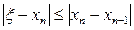 Счет можно прекратить, когда
Счет можно прекратить, когда 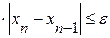
Теорема 2.2: Если 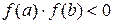 , причем
, причем 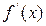 и
и 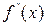 отличны от нуля и сохраняют определенные знаки при
отличны от нуля и сохраняют определенные знаки при 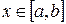 , то, исходя из начального приближения
, то, исходя из начального приближения 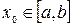 , удовлетворяющего условию
, удовлетворяющего условию 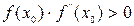 , можно вычислить методом Ньютона единственный корень
, можно вычислить методом Ньютона единственный корень 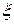 уравнения
уравнения 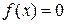 с любой степенью точности.
с любой степенью точности.
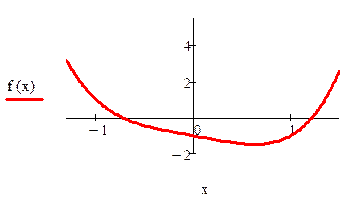
Пример 2.5. Найти методом Ньютона корень уравнения x4-x-1 =0,
| 2-я производная положительна
|
| один корень лежит на промежутке (-1.-0.5), второй на промежутке (1.1.5)
Уточним левый корень методом Ньютона
|
Нашли корень исходного уравнения -0.7245 с точность 0.00007.
Рис. 2.8. Вычисления в Mathcad, реализующие метод касательных для примера 2.5
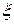 - корень уравнения
- корень уравнения 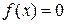 отделен на отрезке
отделен на отрезке 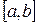 , причем
, причем 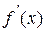 и
и 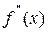 непрерывны и сохраняют определенные знаки на этом же отрезке
непрерывны и сохраняют определенные знаки на этом же отрезке 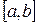 . Найдя какое-нибудь n-е значение корня
. Найдя какое-нибудь n-е значение корня 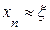 (
(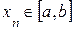 ), уточним его по методу Ньютона. Для этого положим
), уточним его по методу Ньютона. Для этого положим 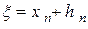 , где
, где 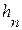 - считаем малой величиной. Разложим функцию f(x) в ряд Тейлора в окрестности точки x n по степеням h n. Тогда можно записать:
- считаем малой величиной. Разложим функцию f(x) в ряд Тейлора в окрестности точки x n по степеням h n. Тогда можно записать: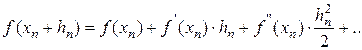
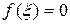 , то:
, то: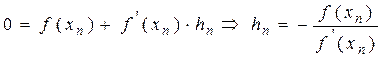 .
.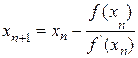 (n=0,1,2,…).
(n=0,1,2,…).
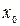 провести касательную к функции f(x), то ее пересечение с осью ОХ и будет новым приближением x1 корня уравнения
провести касательную к функции f(x), то ее пересечение с осью ОХ и будет новым приближением x1 корня уравнения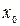 является то значение, для которого выполнено неравенство
является то значение, для которого выполнено неравенство 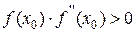 . Погрешность вычислений
. Погрешность вычислений 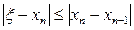 Счет можно прекратить, когда
Счет можно прекратить, когда 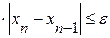
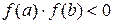 , причем
, причем 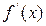 и
и 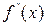 отличны от нуля и сохраняют определенные знаки при
отличны от нуля и сохраняют определенные знаки при 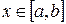 , то, исходя из начального приближения
, то, исходя из начального приближения 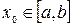 , удовлетворяющего условию
, удовлетворяющего условию 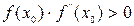 , можно вычислить методом Ньютона единственный корень
, можно вычислить методом Ньютона единственный корень 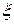 уравнения
уравнения 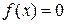 с любой степенью точности.
с любой степенью точности.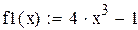
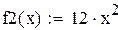
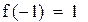
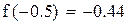
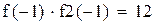
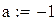
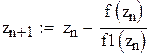

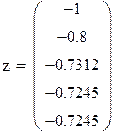
 2015-10-14
2015-10-14 672
672








