В этом методе нелинейная функция f(x) на отделенном промежутке
[ a,b ] заменяется хордой, проходящей через точки (a,f(a))и (b,f(b))
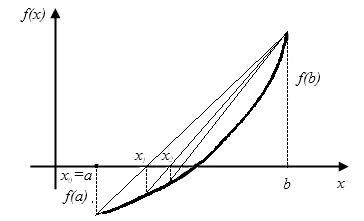
Рис.2.4. Метод хорд. Неподвижен правый конец промежутка b
Уравнение хорды: 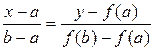 . Найдем точку пересечения хорды с горизонтальной осью. Полагая
. Найдем точку пересечения хорды с горизонтальной осью. Полагая 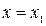 и
и 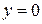 , получим
, получим
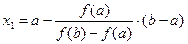 .
.
Точку x1 принимаем за новую границу отрезка, где содержится корень. Через эту точку с координатами (x1,f(x1)) и соответствующую границу предыдущего интервала (b,f(b)) опять проводим хорду, находим 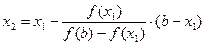 и т.д., получая последовательность x1,x2,x3,…xn,…, сходящуюся к корню уравнения.
и т.д., получая последовательность x1,x2,x3,…xn,…, сходящуюся к корню уравнения.
Вторая производная 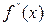 сохраняет постоянный знак на
сохраняет постоянный знак на 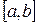 . Следовательно, возможны два случая. Если f(b)·f "(b)>0, то хорда имеет правый фиксированный конец, причем последовательность x0,x1,…xn приближается к корню слева. За начальное приближение x0, естественно, берут a
. Следовательно, возможны два случая. Если f(b)·f "(b)>0, то хорда имеет правый фиксированный конец, причем последовательность x0,x1,…xn приближается к корню слева. За начальное приближение x0, естественно, берут a
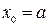 ;
; 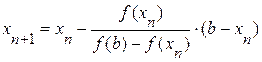 ;
; 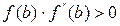 ;
;
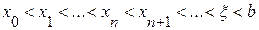 .
.
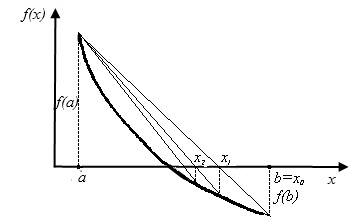
Рис.2.5. Метод хорд. Неподвижен левый конец промежутка a
Если f(a)·f "(a)>0, то хорда имеет левый фиксированный конец, причем последовательность x0,x1,…xn … приближается к корню справа. За начальное приближение x0, берут b
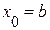 ;
; 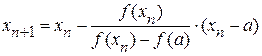 ;
; 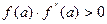 ;
;
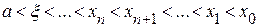 .
.
Для оценки точности можно воспользоваться формулой
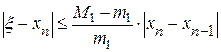 ,
,
где 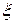 -точный корень,
-точный корень, 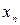 - приближенный корень,
- приближенный корень, 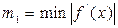 ,
, 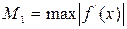 на промежутке [ a,b ]. Считаем до тех пор пока, не выполнится условие
на промежутке [ a,b ]. Считаем до тех пор пока, не выполнится условие 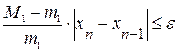 . Если имеет место неравенство
. Если имеет место неравенство 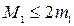 , то счет можно прекратить, когда.
, то счет можно прекратить, когда. 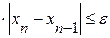
Пример 2.4. Найти методом хорд корень уравнения x4-x-1=0
Решение находим, используя пакет Mathcad.
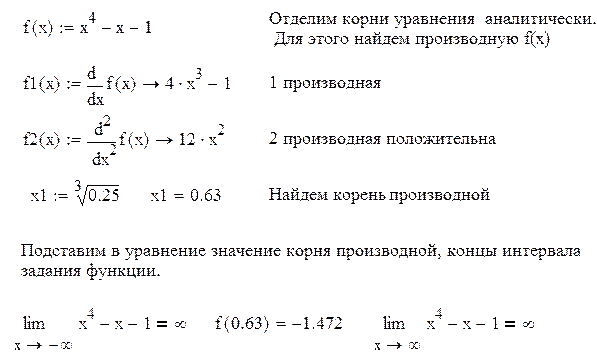
Функция монотонна на промежутках (-∞, 0.63), (0.63, ∞) и меняет на концах промежутков знак. Уравнение имеет два корня. Сузим промежутки отделения корней методом проб, т.е. подстановкой.
Первый корень принадлежит промежутку (-1,-0.5)
Второй корень принадлежит промежутку (1,1.5)
Будем находить корень на промежутке (-1,-0.5)
Вторая производная всюду положительна, функция положительна в точке a = -1, значит, этот конец неподвижен.
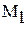 -максимальное, a -максимальное, a 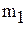 -минимальное значение модуля производной на промежутке -минимальное значение модуля производной на промежутке |
так как 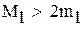 , множитель
, множитель 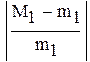
нужно учитывать при оценке точности решения,
Нашли корень исходного уравнения 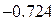 с точностью
с точностью 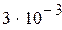 .
.
Рис. 2.6. Вычисления в Mathcad, реализующие метод хорд для примера 2.4

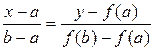 . Найдем точку пересечения хорды с горизонтальной осью. Полагая
. Найдем точку пересечения хорды с горизонтальной осью. Полагая 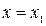 и
и 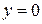 , получим
, получим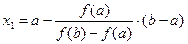 .
.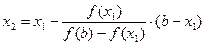 и т.д., получая последовательность x1,x2,x3,…xn,…, сходящуюся к корню уравнения.
и т.д., получая последовательность x1,x2,x3,…xn,…, сходящуюся к корню уравнения.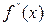 сохраняет постоянный знак на
сохраняет постоянный знак на 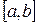 . Следовательно, возможны два случая. Если f(b)·f "(b)>0, то хорда имеет правый фиксированный конец, причем последовательность x0,x1,…xn приближается к корню слева. За начальное приближение x0, естественно, берут a
. Следовательно, возможны два случая. Если f(b)·f "(b)>0, то хорда имеет правый фиксированный конец, причем последовательность x0,x1,…xn приближается к корню слева. За начальное приближение x0, естественно, берут a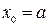 ;
; 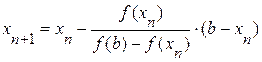 ;
; 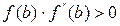 ;
;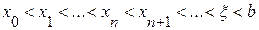 .
.
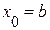 ;
; 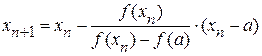 ;
; 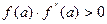 ;
;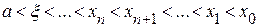 .
.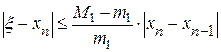 ,
,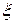 -точный корень,
-точный корень, 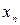 - приближенный корень,
- приближенный корень, 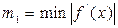 ,
, 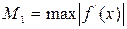 на промежутке [ a,b ]. Считаем до тех пор пока, не выполнится условие
на промежутке [ a,b ]. Считаем до тех пор пока, не выполнится условие 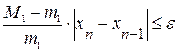 . Если имеет место неравенство
. Если имеет место неравенство 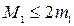 , то счет можно прекратить, когда.
, то счет можно прекратить, когда. 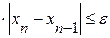
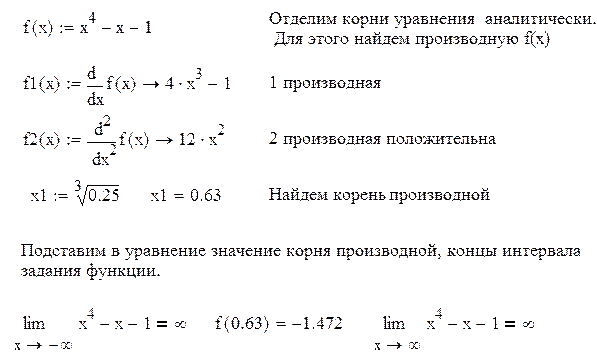
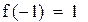
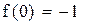
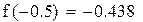
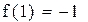
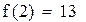
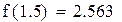
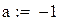
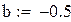
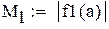
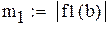
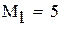
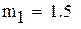
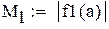
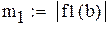
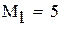
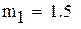
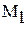 -максимальное, a
-максимальное, a 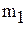 -минимальное значение модуля производной на промежутке
-минимальное значение модуля производной на промежутке 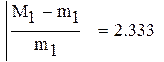
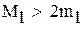 , множитель
, множитель 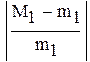
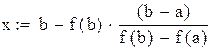
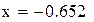
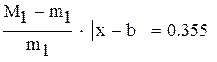
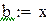
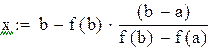
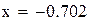
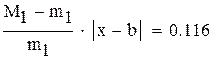
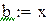
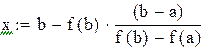
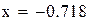
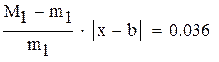
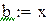
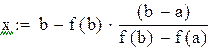
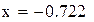
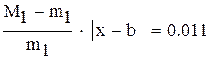
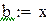
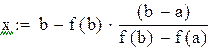
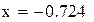
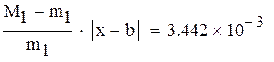
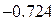 с точностью
с точностью 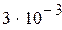 .
. 2015-10-14
2015-10-14 1303
1303
