2015-10-14
388
Для произвольно заданных узлов интерполирования пользуются более общей формулой, так называемой интерполяционной формулой Лагранжа.
Пусть на отрезке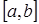 
даны n+1 различных значений аргумента: 
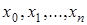, и известны значения для функции 
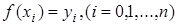. Нам нужно построить многочлен 
.
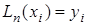Решим сначала частную задачу, построив полином такой, что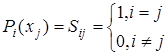 
.
Т.к. искомый полином обращается в нуль в n точках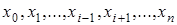 
, то он имеет вид:
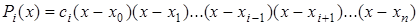, (5.1)
где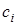 
- постоянный коэффициент. Полагая 
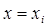в формуле и учитывая, что 
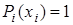, получим:
.
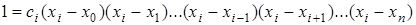Отсюда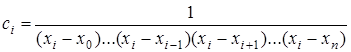 
.
Вернемся к выражению (5.1):
.
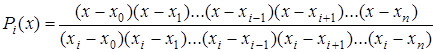Тогда полином Лагранжа имеет следующий вид:
.
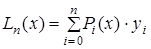Докажем единственность полинома Лагранжа.
Предположим противное. Пусть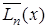 
- полином, отличный от 
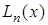, степень его не выше n и 
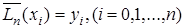. Тогда полином 
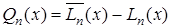, степень которого, очевидно, не выше n, обращается в нуль в n+1 точках 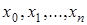, т.е. 
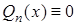. Следовательно, 
.
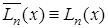При равноотстоящих точках таблицы xi многочлен Лагранжа совпадает с многочленом Ньютона такой же степени.
