Пусть задана система из 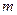 линейных уравнений с
линейных уравнений с 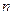 неизвестными
неизвестными 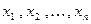 :
:
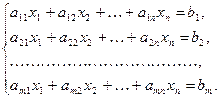 , (3.1)
, (3.1)
где числа 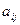 (
(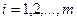 ,
, 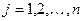 ) называются коэффициентами системы, а числа
) называются коэффициентами системы, а числа 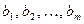 - свободными членами.
- свободными членами.
Решением системы (3.1) называется такой набор чисел 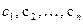 , что при его подстановке в систему вместо соответствующих неизвестных каждое из уравнений обращается в тождество. Если система (3.1) имеет хотя бы одно решение, то она называется совместной; система не имеющая ни одного решения, называется несовместной. Система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. Две системы линейных уравнений с одинаковым числом неизвестных называются эквивалентными, если множества всех решений этих систем совпадают. Если
, что при его подстановке в систему вместо соответствующих неизвестных каждое из уравнений обращается в тождество. Если система (3.1) имеет хотя бы одно решение, то она называется совместной; система не имеющая ни одного решения, называется несовместной. Система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. Две системы линейных уравнений с одинаковым числом неизвестных называются эквивалентными, если множества всех решений этих систем совпадают. Если 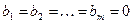 , то система называется однородной, в противном случае она называется неоднородной. Систему (3.1) можно записать в матричной форме:
, то система называется однородной, в противном случае она называется неоднородной. Систему (3.1) можно записать в матричной форме: 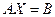 , где
, где
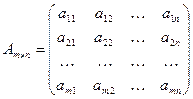 - матрица системы,
- матрица системы,
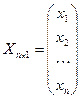 - столбец (или вектор-столбец) неизвестных,
- столбец (или вектор-столбец) неизвестных,
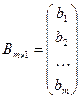 - столбец свободных членов.
- столбец свободных членов.
Матрица 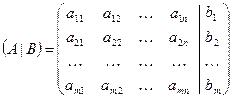 называется расширенной
называется расширенной
матрицей системы.
Рангом матрицы 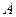 (используют обозначения:
(используют обозначения: 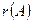 ,
, 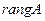 ) называется наибольший из порядков ее миноров, не равных нулю.
) называется наибольший из порядков ее миноров, не равных нулю.
Базисным минором называется любой из отличных от нуля миноров матрицы 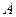 , порядок которого равен
, порядок которого равен 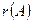 .
.
Э лементарными преобразованиями матриц являются:
· перестановка местами двух параллельных строк (столбцов) матрицы;
· умножение всех элементов строки (столбца) матрицы на число, отличное от нуля;
· прибавление ко всем элементам строки (столбца) матрицы соответствующих элементов другой строки (другого столбца), умноженных на одно и то же число, не равное нулю.
Метод элементарных преобразований при нахождении ранга матрицы заключается в том, что матрицу 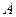 приводят к ступенчатому виду с помощью элементарных преобразований. При исследовании систем линейных уравнений возможны три варианта:
приводят к ступенчатому виду с помощью элементарных преобразований. При исследовании систем линейных уравнений возможны три варианта:
1. Если 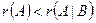 , то система несовместная.
, то система несовместная.
2. Если 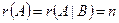 (где
(где 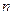 - число неизвестных), то система совместная и определенная.
- число неизвестных), то система совместная и определенная.
3. Если 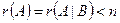 , то система совместная и неопределенная.
, то система совместная и неопределенная.
Для исследования систем линейных уравнений и нахождения их решений, как правило, используют метод Гаусса, формулы Крамера и понятие обратной матрицы.
Задача 3.1. Найти ранг матрицы: 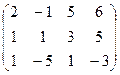 .
.
Решение. 1) Найдем ранг матрицы методом элементарных преобразований, приведя ее к ступенчатому виду. Умножая элементы первой строки матрицы на 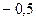 и прибавляя полученный результат ко второй и третьей строкам, получим:
и прибавляя полученный результат ко второй и третьей строкам, получим:
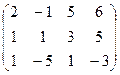 ˜
˜ 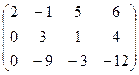 .
.
Умножим вторую строку на 3 и прибавим к третьей строке:
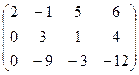 ˜
˜ 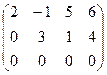 .
.
Полученная ступенчатая матрица содержит две ненулевые строки, поэтому ее ранг равен 2. Следовательно, ранг исходной матрицы также равен 2.
2) Найдем ранг исходной матрицы методом окаймляющих миноров. Так как матрица 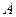 содержит ненулевые элементы, то
содержит ненулевые элементы, то 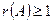 . Выделим какой-либо ненулевой минор 2-го порядка (если он существует). Таким минором является, например,
. Выделим какой-либо ненулевой минор 2-го порядка (если он существует). Таким минором является, например, 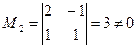 . Следовательно,
. Следовательно, 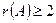 . Так как миноры 3-го порядка, окаймляющие
. Так как миноры 3-го порядка, окаймляющие 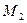 ,
,
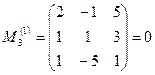 и
и 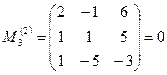 ,
,
то, 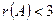 . Получаем, что
. Получаем, что 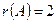 .
.
Задача 3.2. Исследовать систему линейных уравнений; если она совместна, то найти ее общее и одно частное решения:
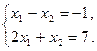
Решение. Запишем расширенную матрицу системы и приведем ее к ступенчатому виду с помощью элементарных преобразований. Умножая первую строку матрицы на 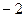 и прибавляя ко второй строке, получим:
и прибавляя ко второй строке, получим:
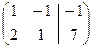 ˜
˜ 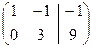 .
.
Ранг матрицы системы равен рангу расширенной матрицы системы: 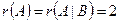 , следовательно, система совместна. Поскольку число неизвестных
, следовательно, система совместна. Поскольку число неизвестных 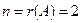 , значит, то система имеет единственное решение.
, значит, то система имеет единственное решение.
Запишем систему уравнений, соответствующую полученной расширенной матрице: 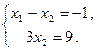 Из второго уравнения
Из второго уравнения 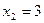 ; подставляя данное значение в первое уравнение, получим
; подставляя данное значение в первое уравнение, получим 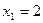 . Итак, общее решение (оно же единственное частное):
. Итак, общее решение (оно же единственное частное): 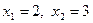 .
.
Задача 3.3. Исследовать систему линейных уравнений; если она совместна, то найти ее общее и одно частное решения: 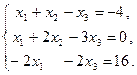
Решение. Приведем к ступенчатому виду расширенную матрицу системы.
Умножая элементы первой строки матрицы на 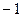 и
и 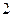 и прибавляя полученные результаты, соответственно, ко второй и третьей строкам, получим:
и прибавляя полученные результаты, соответственно, ко второй и третьей строкам, получим:
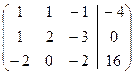 ˜
˜ 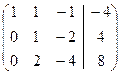 .
.
Вторую строку преобразованной матрицы умножим на 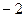 и прибавим к третьей строке:
и прибавим к третьей строке:
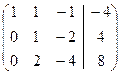 ˜
˜ 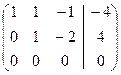 .
.
Так как 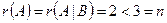 , то система совместна и неопределенна (т.е. имеет бесконечное множество решений). Количество базисных переменных равно
, то система совместна и неопределенна (т.е. имеет бесконечное множество решений). Количество базисных переменных равно 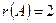 , количество свободных переменных равно
, количество свободных переменных равно 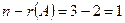 . Выбираем любой не равный нулю минор 2-го порядка преобразованной матрицы
. Выбираем любой не равный нулю минор 2-го порядка преобразованной матрицы 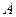 , например, минор
, например, минор 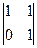 . Переменные
. Переменные 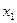 и
и 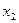 , входящие в него, являются базисными, а
, входящие в него, являются базисными, а 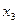 - свободная переменная. Запишем систему уравнений, соответствующую полученной расширенной матрице:
- свободная переменная. Запишем систему уравнений, соответствующую полученной расширенной матрице:
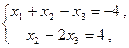 или же
или же 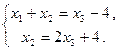
Подставляя выражение для 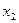 в первое уравнение последней системы, имеем
в первое уравнение последней системы, имеем 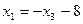 . Обозначая свободную переменную
. Обозначая свободную переменную 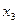 через
через 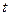 , получим общее решение системы:
, получим общее решение системы: 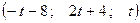 . Частное решение системы легко получить, например, при
. Частное решение системы легко получить, например, при 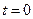 :
: 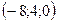 .
.
Задача 3.4. Решить систему уравнений по формулам Крамера и с использованием обратной матрицы:
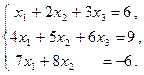
Решение. 1. Решим систему по формулам Крамера: 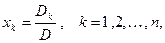 где
где 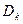 - определитель, полученный из
- определитель, полученный из 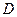 (определителя матрицы
(определителя матрицы 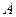 ) заменой
) заменой 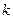 -го столбца столбцом из свободных членов. Запишем определитель матрицы системы:
-го столбца столбцом из свободных членов. Запишем определитель матрицы системы: 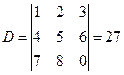 . Так как
. Так как 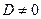 , то решение системы существует и единственно. Найдем определители
, то решение системы существует и единственно. Найдем определители 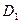 ,
, 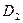 ,
, 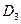 , подставляя столбец свободных членов
, подставляя столбец свободных членов 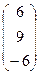 вместо первого, второго и третьего столбцов определителя
вместо первого, второго и третьего столбцов определителя 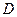 соответственно:
соответственно:
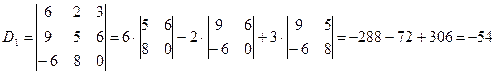 ,
,
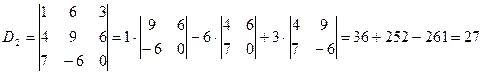 ,
,
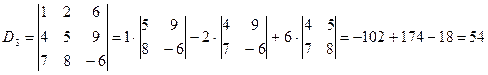 .
.
Следовательно, решение системы уравнений:
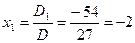 ,
, 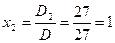 ,
, 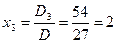 .
.
2. Решим систему с использованием обратной матрицы. С помощью формулы
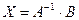 . (3.2)
. (3.2)
Найдем матрицу 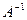 , обратную к матрице системы
, обратную к матрице системы 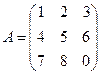 .
.
Так как 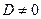 , то матрица
, то матрица 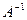 существует. Вычислим алгебраические дополнения всех элементов матрицы
существует. Вычислим алгебраические дополнения всех элементов матрицы 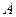 :
:
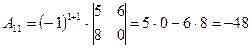 ; ; 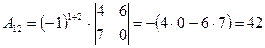 ; ; 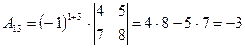 ; ; | 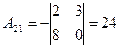 ; ; 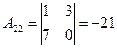 ; ; 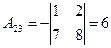 ; ; | 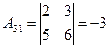 ; ; 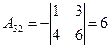 ; ; 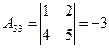 . . |
Запишем присоединенную матрицу 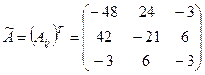 .
.
Найдем матрицу 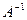 :
:
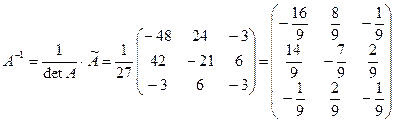 .
.
Сделаем проверку точности вычислений:
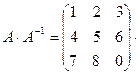
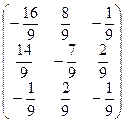 =
= 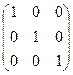 .
.
Теперь решение системы уравнений определяется соотношением:
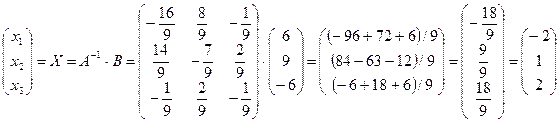 .
.
 2015-10-14
2015-10-14 1058
1058
