Основные понятия по теме

При количественном анализе результатов измерений используют выборки случайных величин. При этом важно организовать экспе­римент таким образом, чтобы вероятность быть выбранным была бы одинакова для любого элемента выборки — так называемая репрезентативная выборка.

При таком подходе точная информация о распределении изучаемых величин отсутствует, поэтому одной из основных задач математи­ческой статистики является оценка числовых характеристик (па­раметров), плотности и функции распределения по отдельным вы­боркам наблюдений.

Оценкой неизвестного параметра θ назы­вают случайную величину 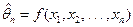, являющуюся функцией наблюденных значений 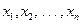. Часто используется так же термин «статистика».

Под статистикой понимают любую функцию от наблю­денных данных. Оценка — это построенная по определенному пра­вилу статистика.

Представление о точности и надежности оценки 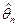связано с понятиями доверительного ин­тервала и доверительной вероятности.

Доверительным интервалом (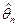 -ε, 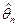+ε) для параметра 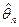называется такой интервал, в пределах которого не­известное значение параметра θ находится с вероятностью γ, не меньшей заданной. Величина γ называется доверительной вероятностью (уровнем доверия) и обычно полагается рав­ной 0,9; 0,95; 0,99. Величину a=1-g называют уровнем значимости.

Среди различных методов нахождения оценок параметров рас­пределений, построенных по выборочным данным, наибольшее применение получил метод моментов.

Суть метода моментов состоит в том, что в силу за­кона больших чисел все выборочные моменты при n→ ∞ сходятся по вероятности к соответствующим моментам исходного распределения. Для вычисления оценок основных числовых характеристик распределения исполь­зуют следующие формулы:

математическое ожидание (среднее)

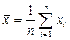; (2.1)

среднеквадратическое отклонение

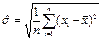; (2.2)

асимметрия

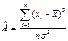; (2.3)

эксцесс

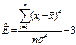. (2.4)

Характеристики, определяемые по выборкам, являются случайными величинами. Следовательно, не­обходимо указать их оценки и соответствующие этим оценкам до­верительные интервалы. Для математического ожидания доверительный интервал имеет вид:

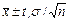, (2.5)

где 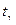- g-квантиль центрированного нормированного нормального распределения.

Статистическими оценками фун­кции F(х) и плотности f(х) рас­пределения являются соответствен­но статистическая функция рас­пределения (называемая также выборочной функцией распределения, функцией накопленных частот, кумулятивной кривой) и гистограмма.

Под статистической функцией распреде­ления случайной величины понимается частота события, что Х<x, т. е.

.

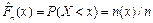Для нахождения этой функции при фиксированном х следует найти число значений СВ, меньших х, а затем по­лученный результат разделить на общее число значений случайной величины n. Функция F_n(x) представляет дискретную ступенча­тую функцию, скачки которой соответствуют значениям X и равны частотам этих значений (рисунок 2).

Гистограмма описывает распределение частот p_i=m_i/n определяемых для каждого значения х_i случайной величины Х..

Для построения гистограммы весь диапазон значений Х разби­вается на некоторое число градаций (разрядов) и подсчитывается число значений случайной величины m_i приходящееся на каждую i-ю градацию, которое затем нормируется по общему числу значе­ний n. По оси абсцисс откладываются градации (разряды), а по оси ординат — соответствующие этим разрядам частоты р_i, называемые иногда частостями (рисунок 1).

При построении гистограмм не существует строго обоснованных методов определения числа разрядов r. Обычно пользуются одним из трех эмпирических правил: 1) определяют 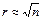; 2) г нахо­дят по интервалу группирования исходных данных Δx, равного погрешности (двойной или тройной ее величине) измерения пара­метра; 3) r определяют по величине Δx, вычисляемой по формуле Стерджеса

.

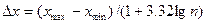При этом в каждом разряде гистограммы не должно быть менее пяти значений, в противном случае проводится объединение не­скольких разрядов. Общее число разрядов также должно быть не менее пяти.

Пример 1 В результате n = 100 измерений плотности горной по­роды на денситометре с погрешностью δ = ±0,01 г/см³ получены данные, приведенные в таблице 3.

Таблица 3 – Данные измерений

Плотность, г/см3	Частость mi	Плотность, г/см3	Частость mi	Плотность, г/см3	Частость mi
2.00		2.06		2.12
2.01		2.07		2.13
2.02		2.08		2.14
2.03		2.09		2.15
2.04		2.10		2.16
2.05		2.11		2.17
-	-	-	-	2.18

Определить оценки среднего значения плотности, среднеквадратического отклонения, асимметрии и эксцесса. Построить статистическую функцию распределения и гистограмму. Для среднего значения определить доверительный интервал с уровнем доверия 95 %.

По данным таблицы 3 находим оценки среднего значения и среднеквадратического отклонения (в г/см⁸):

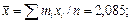
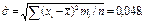
Оценки асимметрии и эксцесса:

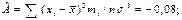
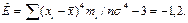
Доверительный интервал определяем из выражения ,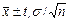

где t_γ - γ-квантиль (0,1) нормального распределения. По таблице функции Лапласа для γ=0,95 получаем t_γ =1,65. Тогда доверительный интервал будет: 2,085±0,0079.

Для построения оценки плотности распределения — гистограммы не­обходимо провести группирование данных по разрядам. По формуле Стерджеса имеем

.

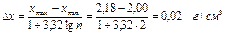Такой, же интервал группирования получаем, исходя из равенства ин­тервала двойной погрешности измерений: Δx=2δ= 0,02 г/см³. Проведем группирование данных, учитывая, что в каждом разряде гистограммы не должно быть менее пяти значений. В результате объединения значений плотности по разрядам получим гистограмму, значения которой даны в табл. 4 (столбец 4), а ее график — на рисунке 1.

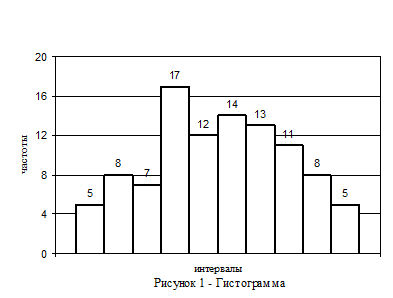
Таблица 4 – Результаты статистической обработки данных

Разряд	Граница интервала, г/см3	Частота в интервале	Накопленные частоты
xi	xi+1
	-∞	2,00
	2,00	2,02
	2,02	2,04
	2,04	2,06
	2,06	2,08
	2,08	2,10
	2,10	2,12
	2,12	2,14
	2,14	2,16
	1,16	∞

По накопленным частотам (столбец 5 таблицы 4) строится статистическая функция распределения (рисунок 2).

Вопросы для самоконтроля

1 Что понимается под статистической оценкой случайной величины?

2 Что такое доверительный интервал и доверительная вероятность?

3 Привести формулы расчета статистических оценок основных числовых характеристик случайной величины.

4 Как построить статистическую функцию распределения?

5 Как строится гистограмма?