Балка АВ закреплена в точке А с помощью неподвижного шарнира и удерживается в горизонтальном положении подвижным цилиндрическим шарниром в точке В (рис. 1.18). В середине балки действует сила Р=2 кН под углом 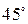 к горизонту. Определить реакции опор, взяв размеры из рисунка и пренебрегая весом балки.
к горизонту. Определить реакции опор, взяв размеры из рисунка и пренебрегая весом балки.
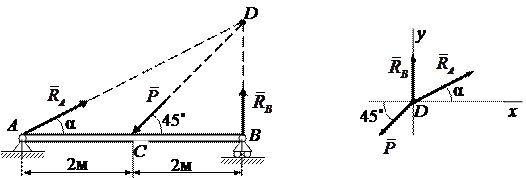
а) б)
Рисунок 1.18
Решение
Балка находится в равновесии под действием трех сил: активной силы 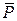 и реакций
и реакций 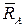 и
и 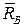 . Реакция
. Реакция 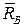 подвижного шарнира В направлена перпендикулярно опорной поверхности по вертикали. Реакция
подвижного шарнира В направлена перпендикулярно опорной поверхности по вертикали. Реакция 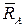 шарнира А согласно теореме о трех силах пройдет через точку D пересечения сил
шарнира А согласно теореме о трех силах пройдет через точку D пересечения сил 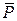 и
и 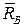 , создав угол
, создав угол 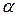 с горизонталью.
с горизонталью.
Величину угла 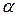 найдем, рассмотрев прямоугольный треугольник АВD, в котором катет
найдем, рассмотрев прямоугольный треугольник АВD, в котором катет 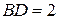 м (как катет равнобедренного треугольника ВСD), а гипотенуза
м (как катет равнобедренного треугольника ВСD), а гипотенуза
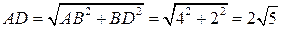 м.
м.
Тогда 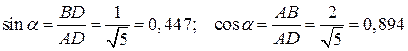 .
.
Перенесем все силы в точку D (рис. 1.18,б) и составим уравнение равновесия плоской системы совпадающих сил:
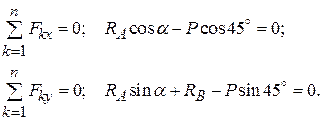
Отсюда получим:
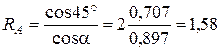 кН;
кН;
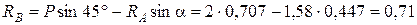 кН.
кН.
 2015-10-14
2015-10-14 353
353








